From 913587913cd549020dcb172dad8a96cbe5a9bf97 Mon Sep 17 00:00:00 2001
From: Michael Abbott <32575566+mcabbott@users.noreply.github.com>
Date: Sat, 26 Nov 2022 23:21:57 -0500
Subject: [PATCH 01/10] Delete tutorialposts directory
---
.../2020-09-15-deep-learning-flux.md | 435 ------------------
tutorialposts/2020-10-18-transfer-learning.md | 93 ----
tutorialposts/2021-01-21-data-loader.md | 79 ----
tutorialposts/2021-01-26-mlp.md | 169 -------
tutorialposts/2021-02-07-convnet.md | 261 -----------
tutorialposts/2021-10-08-dcgan-mnist.md | 369 ---------------
tutorialposts/2021-10-14-vanilla-gan.md | 283 ------------
7 files changed, 1689 deletions(-)
delete mode 100755 tutorialposts/2020-09-15-deep-learning-flux.md
delete mode 100644 tutorialposts/2020-10-18-transfer-learning.md
delete mode 100755 tutorialposts/2021-01-21-data-loader.md
delete mode 100644 tutorialposts/2021-01-26-mlp.md
delete mode 100644 tutorialposts/2021-02-07-convnet.md
delete mode 100644 tutorialposts/2021-10-08-dcgan-mnist.md
delete mode 100644 tutorialposts/2021-10-14-vanilla-gan.md
diff --git a/tutorialposts/2020-09-15-deep-learning-flux.md b/tutorialposts/2020-09-15-deep-learning-flux.md
deleted file mode 100755
index 5747516b..00000000
--- a/tutorialposts/2020-09-15-deep-learning-flux.md
+++ /dev/null
@@ -1,435 +0,0 @@
-+++
-title = "Deep Learning with Flux - A 60 Minute Blitz"
-published = "15 November 2020"
-author = "Saswat Das, Mike Innes, Andrew Dinhobl, Ygor Canalli, Sudhanshu Agrawal, João Felipe Santos"
-+++
-
-This is a quick intro to [Flux](https://github.com/FluxML/Flux.jl) loosely based on [PyTorch's tutorial](https://pytorch.org/tutorials/beginner/deep_learning_60min_blitz.html). It introduces basic Julia programming, as well Zygote, a source-to-source automatic differentiation (AD) framework in Julia. We'll use these tools to build a very simple neural network.
-
-## Arrays
-
-The starting point for all of our models is the `Array` (sometimes referred to as a `Tensor` in other frameworks). This is really just a list of numbers, which might be arranged into a shape like a square. Let's write down an array with three elements.
-
-```julia
-x = [1, 2, 3]
-```
-
-Here's a matrix – a square array with four elements.
-
-```julia
-x = [1 2; 3 4]
-```
-
-We often work with arrays of thousands of elements, and don't usually write them down by hand. Here's how we can create an array of 5×3 = 15 elements, each a random number from zero to one.
-
-```julia
-x = rand(5, 3)
-```
-
-There's a few functions like this; try replacing `rand` with `ones`, `zeros`, or `randn` to see what they do.
-
-By default, Julia works stores numbers is a high-precision format called `Float64`. In ML we often don't need all those digits, and can ask Julia to work with `Float32` instead. We can even ask for more digits using `BigFloat`.
-
-```julia
-x = rand(BigFloat, 5, 3)
-
-x = rand(Float32, 5, 3)
-```
-
-We can ask the array how many elements it has.
-
-```julia
-length(x)
-```
-
-Or, more specifically, what size it has.
-
-```julia
-size(x)
-```
-
-We sometimes want to see some elements of the array on their own.
-
-```julia
-x
-
-x[2, 3]
-```
-
-This means get the second row and the third column. We can also get every row of the third column.
-
-```julia
-x[:, 3]
-```
-
-We can add arrays, and subtract them, which adds or subtracts each element of the array.
-
-```julia
-x + x
-
-x - x
-```
-
-Julia supports a feature called *broadcasting*, using the `.` syntax. This tiles small arrays (or single numbers) to fill bigger ones.
-
-```julia
-x .+ 1
-```
-
-We can see Julia tile the column vector `1:5` across all rows of the larger array.
-
-```julia
-zeros(5,5) .+ (1:5)
-```
-
-The x' syntax is used to transpose a column `1:5` into an equivalent row, and Julia will tile that across columns.
-
-```julia
-zeros(5,5) .+ (1:5)'
-```
-
-We can use this to make a times table.
-
-```julia
-(1:5) .* (1:5)'
-```
-
-Finally, and importantly for machine learning, we can conveniently do things like matrix multiply.
-
-```julia
-W = randn(5, 10)
-x = rand(10)
-W * x
-```
-
-Julia's arrays are very powerful, and you can learn more about what they can do [here](https://docs.julialang.org/en/v1/manual/arrays/).
-
-## CUDA Arrays
-
-CUDA functionality is provided separately by the [CUDA package](https://github.com/JuliaGPU/CUDA.jl). If you have a GPU and CUDA available, you can run `] add CUDA` in a REPL or IJulia to get it.
-
-Once CUDA is loaded you can move any array to the GPU with the `cu` function, and it supports all of the above operations with the same syntax.
-
-```julia
-using CUDA
-x = cu(rand(5, 3))
-```
-
-## Automatic Differentiation
-
-You probably learned to take derivatives in school. We start with a simple mathematical function like
-
-```julia
-f(x) = 3x^2 + 2x + 1
-
-f(5)
-```
-
-In simple cases it's pretty easy to work out the gradient by hand – here it's `6x+2`. But it's much easier to make Flux do the work for us!
-
-```julia
-using Flux: gradient
-
-df(x) = gradient(f, x)[1]
-
-df(5)
-```
-
-You can try this with a few different inputs to make sure it's really the same as `6x+2`. We can even do this multiple times (but the second derivative is a fairly boring `6`).
-
-```julia
-ddf(x) = gradient(df, x)[1]
-
-ddf(5)
-```
-
-Flux's AD can handle any Julia code you throw at it, including loops, recursion and custom layers, so long as the mathematical functions you call are differentiable. For example, we can differentiate a Taylor approximation to the `sin` function.
-
-```julia
-mysin(x) = sum((-1)^k*x^(1+2k)/factorial(1+2k) for k in 0:5)
-
-x = 0.5
-
-mysin(x), gradient(mysin, x)
-
-sin(x), cos(x)
-```
-
-You can see that the derivative we calculated is very close to `cos(x)`, as we expect.
-
-This gets more interesting when we consider functions that take *arrays* as inputs, rather than just a single number. For example, here's a function that takes a matrix and two vectors (the definition itself is arbitrary)
-
-```julia
-myloss(W, b, x) = sum(W * x .+ b)
-
-W = randn(3, 5)
-b = zeros(3)
-x = rand(5)
-
-gradient(myloss, W, b, x)
-```
-
-Now we get gradients for each of the inputs `W`, `b` and `x`, which will come in handy when we want to train models.
-
-Because ML models can contain hundreds of parameters, Flux provides a slightly different way of writing `gradient`. We instead mark arrays with `param` to indicate that we want their derivatives. `W` and `b` represent the weight and bias respectively.
-
-```julia
-using Flux: params
-
-W = randn(3, 5)
-b = zeros(3)
-x = rand(5)
-
-y(x) = sum(W * x .+ b)
-
-grads = gradient(()->y(x), params([W, b]))
-
-grads[W], grads[b]
-```
-
-
-We can now grab the gradients of `W` and `b` directly from those parameters.
-
-This comes in handy when working with *layers*. A layer is just a handy container for some parameters. For example, `Dense` does a linear transform for you.
-
-```julia
-using Flux
-
-m = Dense(10, 5)
-
-x = rand(Float32, 10)
-```
-
-We can easily get the parameters of any layer or model with params with `params`.
-
-```julia
-params(m)
-```
-
-This makes it very easy to calculate the gradient for all parameters in a network, even if it has many parameters.
-
-```julia
-x = rand(Float32, 10)
-m = Chain(Dense(10, 5, relu), Dense(5, 2), softmax)
-l(x) = sum(Flux.crossentropy(m(x), [0.5, 0.5]))
-grads = gradient(params(m)) do
- l(x)
-end
-for p in params(m)
- println(grads[p])
-end
-```
-
-You don't have to use layers, but they can be convient for many simple kinds of models and fast iteration.
-
-The next step is to update our weights and perform optimisation. As you might be familiar, *Gradient Descent* is a simple algorithm that takes the weights and steps using a learning rate and the gradients. `weights = weights - learning_rate * gradient`.
-
-```julia
-using Flux.Optimise: update!, Descent
-η = 0.1
-for p in params(m)
- update!(p, -η * grads[p])
-end
-```
-
-While this is a valid way of updating our weights, it can get more complicated as the algorithms we use get more involved.
-
-Flux comes with a bunch of pre-defined optimisers and makes writing our own really simple. We just give it the learning rate η:
-
-```julia
-opt = Descent(0.01)
-```
-
-`Training` a network reduces down to iterating on a dataset mulitple times, performing these steps in order. Just for a quick implementation, let’s train a network that learns to predict `0.5` for every input of 10 floats. `Flux` defines the `train!` function to do it for us.
-
-```julia
-data, labels = rand(10, 100), fill(0.5, 2, 100)
-loss(x, y) = sum(Flux.crossentropy(m(x), y))
-Flux.train!(loss, params(m), [(data,labels)], opt)
-```
-
-You don't have to use `train!`. In cases where aribtrary logic might be better suited, you could open up this training loop like so:
-
-```julia
- for d in training_set # assuming d looks like (data, labels)
- # our super logic
- gs = gradient(params(m)) do #m is our model
- l = loss(d...)
- end
- update!(opt, params(m), gs)
- end
-```
-
-## Training a Classifier
-
-Getting a real classifier to work might help cement the workflow a bit more. [CIFAR10](https://https://www.cs.toronto.edu/~kriz/cifar.html) is a dataset of 50k tiny training images split into 10 classes.
-
-We will do the following steps in order:
-
-* Load CIFAR10 training and test datasets
-* Define a Convolution Neural Network
-* Define a loss function
-* Train the network on the training data
-* Test the network on the test data
-
-### Loading the Dataset
-
-```julia
-using Statistics
-using Flux, Flux.Optimise
-using MLDatasets: CIFAR10
-using Images.ImageCore
-using Flux: onehotbatch, onecold
-using Base.Iterators: partition
-using CUDA
-```
-
-This image will give us an idea of what we are dealing with.
-
-
-
-```julia
-train_x, train_y = CIFAR10.traindata(Float32)
-labels = onehotbatch(train_y, 0:9)
-```
-
-The `train_x` contains 50000 images converted to 32 X 32 X 3 arrays with the third dimension being the 3 channels (R,G,B). Let's take a look at a random image from the train_x. For this, we need to permute the dimensions to 3 X 32 X 32 and use `colorview` to convert it back to an image.
-
-```julia
-using Plots
-image(x) = colorview(RGB, permutedims(x, (3, 2, 1)))
-plot(image(train_x[:,:,:,rand(1:end)]))
-```
-
-We can now arrange the training data in batches of say, 1000 and keep a validation set to track our progress. This process is called minibatch learning, which is a popular method of training large neural networks. Rather that sending the entire dataset at once, we break it down into smaller chunks (called minibatches) that are typically chosen at random, and train only on them. It is shown to help with escaping [saddle points](https://en.wikipedia.org/wiki/Saddle_point).
-
-The first 49k images (in batches of 1000) will be our training set, and the rest is for validation. `partition` handily breaks down the set we give it in consecutive parts (1000 in this case).
-
-```julia
-train = ([(train_x[:,:,:,i], labels[:,i]) for i in partition(1:49000, 1000)]) |> gpu
-valset = 49001:50000
-valX = train_x[:,:,:,valset] |> gpu
-valY = labels[:, valset] |> gpu
-```
-
-### Defining the Classifier
-
-Now we can define our Convolutional Neural Network (CNN).
-
-A convolutional neural network is one which defines a kernel and slides it across a matrix to create an intermediate representation to extract features from. It creates higher order features as it goes into deeper layers, making it suitable for images, where the strucure of the subject is what will help us determine which class it belongs to.
-
-```julia
-m = Chain(
- Conv((5,5), 3=>16, relu),
- MaxPool((2,2)),
- Conv((5,5), 16=>8, relu),
- MaxPool((2,2)),
- x -> reshape(x, :, size(x, 4)),
- Dense(200, 120),
- Dense(120, 84),
- Dense(84, 10),
- softmax) |> gpu
-```
-
-We will use a crossentropy loss and an Momentum optimiser here. Crossentropy will be a good option when it comes to working with mulitple independent classes. Momentum gradually lowers the learning rate as we proceed with the training. It helps maintain a bit of adaptivity in our optimisation, preventing us from over shooting from our desired destination.
-
-```julia
-using Flux: crossentropy, Momentum
-
-loss(x, y) = sum(crossentropy(m(x), y))
-opt = Momentum(0.01)
-```
-
-We can start writing our train loop where we will keep track of some basic accuracy numbers about our model. We can define an `accuracy` function for it like so.
-
-```julia
-accuracy(x, y) = mean(onecold(m(x), 0:9) .== onecold(y, 0:9))
-```
-
-### Training the Classifier
-
-
-Training is where we do a bunch of the interesting operations we defined earlier, and see what our net is capable of. We will loop over the dataset 10 times and feed the inputs to the neural network and optimise.
-
-```julia
-epochs = 10
-
-for epoch = 1:epochs
- for d in train
- gs = gradient(params(m)) do
- l = loss(d...)
- end
- update!(opt, params(m), gs)
- end
- @show accuracy(valX, valY)
-end
-```
-
-Seeing our training routine unfold gives us an idea of how the network learnt the function. This is not bad for a small hand-written network, trained for a limited time.
-
-### Training on a GPU
-
-The `gpu` functions you see sprinkled through this bit of the code tell Flux to move these entities to an available GPU, and subsequently train on it. No extra faffing about required! The same bit of code would work on any hardware with some small annotations like you saw here.
-
-### Testing the Network
-
-We have trained the network for 100 passes over the training dataset. But we need to check if the network has learnt anything at all.
-
-We will check this by predicting the class label that the neural network outputs, and checking it against the ground-truth. If the prediction is correct, we add the sample to the list of correct predictions. This will be done on a yet unseen section of data.
-
-Okay, first step. Let us perform the exact same preprocessing on this set, as we did on our training set.
-
-```julia
-test_x, test_y = CIFAR10.testdata(Float32)
-test_labels = onehotbatch(test_y, 0:9)
-
-test = gpu.([(test_x[:,:,:,i], test_labels[:,i]) for i in partition(1:10000, 1000)])
-```
-
-Next, display an image from the test set.
-
-```julia
-plot(image(test_x[:,:,:,rand(1:end)]))
-```
-
-The outputs are energies for the 10 classes. Higher the energy for a class, the more the network thinks that the image is of the particular class. Every column corresponds to the output of one image, with the 10 floats in the column being the energies.
-
-Let's see how the model fared.
-
-```julia
-ids = rand(1:10000, 5)
-rand_test = test_x[:,:,:,ids] |> gpu
-rand_truth = test_y[ids]
-m(rand_test)
-```
-
-This looks similar to how we would expect the results to be. At this point, it's a good idea to see how our net actually performs on new data, that we have prepared.
-
-```julia
-accuracy(test[1]...)
-```
-
-This is much better than random chance set at 10% (since we only have 10 classes), and not bad at all for a small hand written network like ours.
-
-Let's take a look at how the net performed on all the classes performed individually.
-
-```julia
-class_correct = zeros(10)
-class_total = zeros(10)
-for i in 1:10
- preds = m(test[i][1])
- lab = test[i][2]
- for j = 1:1000
- pred_class = findmax(preds[:, j])[2]
- actual_class = findmax(lab[:, j])[2]
- if pred_class == actual_class
- class_correct[pred_class] += 1
- end
- class_total[actual_class] += 1
- end
-end
-
-class_correct ./ class_total
-```
-
-The spread seems pretty good, with certain classes performing significantly better than the others. Why should that be?
diff --git a/tutorialposts/2020-10-18-transfer-learning.md b/tutorialposts/2020-10-18-transfer-learning.md
deleted file mode 100644
index 95f16c40..00000000
--- a/tutorialposts/2020-10-18-transfer-learning.md
+++ /dev/null
@@ -1,93 +0,0 @@
-+++
-title = "Transfer Learning with Flux"
-published = "18 October 2020"
-author = "Dhairya Gandhi"
-+++
-
-This article is intended to be a general guide to how transfer learning works in the Flux ecosystem. We assume a certain familiarity of the reader with the concept of transfer learning. Having said that, we will start off with a basic definition of the setup and what we are trying to achieve. There are many resources online that go in depth as to why transfer learning is an effective tool to solve many ML problems, and we recommend checking some of those out.
-
-Machine Learning today has evolved to use many highly trained models in a general task, where they are tuned to perform especially well on a subset of the problem.
-
-This is one of the key ways in which larger (or smaller) models are used in practice. They are trained on a general problem, achieving good results on the test set, and then subsequently tuned on specialised datasets.
-
-In this process, our model is already pretty well trained on the problem, so we don't need to train it all over again as if from scratch. In fact, as it so happens, we don't need to do that at all! We only need to tune the last couple of layers to get the most performance from our models. The exact last number of layers is dependant on the problem setup and the expected outcome, but a common tip is to train the last few `Dense` layers in a more complicated model.
-
-So let's try to simulate the problem in Flux.
-
-We'll tune a pretrained ResNet from Metalhead as a proxy. We will tune the `Dense` layers in there on a new set of images.
-
-```julia
-using Flux, Metalhead
-using Flux: @epochs
-using Metalhead.Images
-resnet = ResNet().layers
-```
-
-If we intended to add a new class of objects in there, we need only `reshape` the output from the previous layers accordingly.
-Our model would look something like so:
-
-```julia
- model = Chain(
- resnet[1:end-2], # We only need to pull out the dense layer in here
- x -> reshape(x, size_we_want), # / global_avg_pooling layer
- Dense(reshaped_input_features, n_classes)
- )
-```
-
-We will use the [Dogs vs. Cats](https://www.kaggle.com/c/dogs-vs-cats/data?select=train.zip) dataset from Kaggle for our use here.
-Make sure to download the `train.zip` file and extract it into a `train` folder.
-
-The [`dataloader.jl`](https://github.com/FluxML/model-zoo/blob/master/tutorials/transfer_learning/dataloader.jl) script contains a pre-written `load_batch` function which will load a set of images, shuffled between dogs and cats along with their correct labels.
-
-```julia
-include("dataloader.jl")
-```
-
-Finally, the model looks something like:
-
-```julia
-model = Chain(
- resnet[1:end-2],
- Dense(2048, 1000),
- Dense(1000, 256),
- Dense(256, 2), # we get 2048 features out, and we have 2 classes
-)
-```
-
-To speed up training, let’s move everything over to the GPU
-
-```julia
-model = model |> gpu
-dataset = [gpu.(load_batch(10)) for i in 1:10]
-```
-
-After this, we only need to define the other parts of the training pipeline like we usually do.
-
-```julia
-opt = ADAM()
-loss(x,y) = Flux.Losses.logitcrossentropy(model(x), y)
-```
-
-Now to train. As discussed earlier, we don’t need to pass all the parameters to our training loop. Only the ones we need to fine-tune. Note that we could have picked and chosen the layers we want to train individually as well, but this is sufficient for our use as of now.
-
-```julia
-ps = Flux.params(model)
-```
-**Note**: Normally, you would only re-train the dense layers via `model[2:end]` but in this case, the pre-trained models from Metalhead.jl are not currently available. This will change in the future once the pre-trained models are once again available.
-
-And now, let's train!
-
-```julia
-@epochs 2 Flux.train!(loss, ps, dataset, opt)
-```
-
-And there you have it, a pretrained model, fine tuned to tell the the dogs from the cats.
-
-We can verify this too.
-
-```julia
-imgs, labels = gpu.(load_batch(10))
-display(model(imgs))
-
-labels
-```
diff --git a/tutorialposts/2021-01-21-data-loader.md b/tutorialposts/2021-01-21-data-loader.md
deleted file mode 100755
index 6352c20e..00000000
--- a/tutorialposts/2021-01-21-data-loader.md
+++ /dev/null
@@ -1,79 +0,0 @@
-+++
-title = "Using Flux DataLoader"
-published = "21 January 2021"
-author = "Liliana Badillo, Dhairya Gandhi"
-+++
-
-In this tutorial, we show how to load image data in Flux DataLoader and process it in mini-batches. We use the [DataLoader](https://fluxml.ai/Flux.jl/stable/data/dataloader/#Flux.Data.DataLoader) type to handle iteration over mini-batches of data. For this example, we load the [MNIST dataset](https://juliaml.github.io/MLDatasets.jl/stable/datasets/MNIST/) using the [MLDatasets](https://juliaml.github.io/MLDatasets.jl/stable/) package.
-
-Before we start, make sure you have installed the following packages:
-
-* [Flux](https://github.com/FluxML/Flux.jl)
-* [MLDatasets](https://juliaml.github.io/MLDatasets.jl/stable/)
-
-To install these packages, run the following in the REPL:
-
-```julia
-Pkg.add("Flux")
-Pkg.add("MLDatasets")
-```
-
-Load the packages we'll need:
-
-```julia
-using MLDatasets: MNIST
-using Flux.Data: DataLoader
-using Flux: onehotbatch
-```
-
-## Step1: Loading the MNIST data set
-
-We load the MNIST train and test data from MLDatasets:
-
-```julia
-train_x, train_y = MNIST(:train)[:]
-test_x, test_y = MNIST(:test)[:]
-```
-
-This code loads the MNIST train and test images as Float32 as well as their labels. The data set `train_x` is a 28×28×60000 multi-dimensional array. It contains 60000 elements and each one of it contains a 28x28 array. Each array represents a 28x28 image (in grayscale) of a handwritten digit. Moreover, each element of the 28x28 arrays is a pixel that represents the amount of light that it contains. On the other hand, `test_y` is a 60000 element vector and each element of this vector represents the label or actual value (0 to 9) of a handwritten digit.
-
-## Step 2: Loading the dataset onto DataLoader
-
-Before we load the data onto a DataLoader, we need to reshape it so that it has the correct shape for Flux. For this example, the MNIST train data must be of the same dimension as our model's input and output layers.
-
-For example, if our model's input layer expects a 28x28x1 multi-dimensional array, we need to reshape the train and test data as follows:
-
-```julia
-train_x = reshape(train_x, 28, 28, 1, :)
-test_x = reshape(test_x, 28, 28, 1, :)
-```
-
-Also, the MNIST labels must be encoded as a vector with the same dimension as the number of categories (unique handwritten digits) in the data set. To encode the labels, we use the [Flux's onehotbatch](https://fluxml.ai/Flux.jl/stable/data/onehot/#Batches-1) function:
-
-```julia
-train_y, test_y = onehotbatch(train_y, 0:9), onehotbatch(test_y, 0:9)
-```
-
->**Note:** For more information on other encoding methods, see [Handling Data in Flux](https://fluxml.ai/Flux.jl/stable/data/onehot/).
-
-Now, we load the train images and their labels onto a DataLoader object:
-
-```julia
-data_loader = DataLoader((train_x, train_y); batchsize=128, shuffle=true)
-```
-
-Notice that we set the DataLoader `batchsize` to 128. This will enable us to iterate over the data in batches of size 128. Also, by setting `shuffle=true` the DataLoader will shuffle the observations each time that iterations are re-started.
-
-## Step 3: Iterating over the data
-
-Finally, we can iterate over the 60000 MNIST train data in mini-batches (most of them of size 128) using the Dataloader that we created in the previous step. Each element of the DataLoader is a tuple `(x, y)` in which `x` represents a 28x28x1 array and `y` a vector that encodes the corresponding label of the image.
-
-```julia
-for (x, y) in data_loader
- @assert size(x) == (28, 28, 1, 128) || size(x) == (28, 28, 1, 96)
- @assert size(y) == (10, 128) || size(y) == (10, 96)
- ...
-end
-```
-
-Now, we can create a model and train it using the `data_loader` we just created. For more information on building models in Flux, see [Model-Building Basics](https://fluxml.ai/Flux.jl/stable/models/basics/#Model-Building-Basics-1).
diff --git a/tutorialposts/2021-01-26-mlp.md b/tutorialposts/2021-01-26-mlp.md
deleted file mode 100644
index 2257c93b..00000000
--- a/tutorialposts/2021-01-26-mlp.md
+++ /dev/null
@@ -1,169 +0,0 @@
-+++
-title = "Simple multi-layer perceptron"
-published = "26 January 2021"
-author = "Adarsh Kumar, Mike J Innes, Andrew Dinhobl, Jerry Ling, natema, Zhang Shitian, Liliana Badillo, Dhairya Gandhi"
-+++
-
-In this example, we create a simple [multi-layer perceptron](https://en.wikipedia.org/wiki/Multilayer_perceptron#:~:text=A%20multilayer%20perceptron%20(MLP)%20is,artificial%20neural%20network%20(ANN).&text=An%20MLP%20consists%20of%20at,uses%20a%20nonlinear%20activation%20function.) (MLP) that classifies handwritten digits using the MNIST dataset. A MLP consists of at least *three layers* of stacked perceptrons: Input, hidden, and output. Each neuron of an MLP has parameters (weights and bias) and uses an [activation function](https://en.wikipedia.org/wiki/Activation_function) to compute its output.
-
-To run this example, we need the following packages:
-
-```julia
-using Flux, Statistics
-using Flux.Data: DataLoader
-using Flux: onehotbatch, onecold, logitcrossentropy, throttle, @epochs
-using Base.Iterators: repeated
-using Parameters: @with_kw
-using CUDA
-using MLDatasets
-if has_cuda() # Check if CUDA is available
- @info "CUDA is on"
- CUDA.allowscalar(false)
-end
-```
-
-We set default values for learning rate, batch size, epochs, and the usage of a GPU (if available) for our model:
-
-```julia
-@with_kw mutable struct Args
- η::Float64 = 3e-4 # learning rate
- batchsize::Int = 1024 # batch size
- epochs::Int = 10 # number of epochs
- device::Function = gpu # set as gpu, if gpu available
-end
-```
-
-
-If a GPU is available on our local system, then Flux uses it for computing the loss and updating the weights and biases when training our model.
-
-## Data
-
-We create the function `getdata` to load the MNIST train and test data sets from [MLDatasets](https://juliaml.github.io/MLDatasets.jl/latest/) and prepare them for the training process. In addition, we set mini-batches of the data sets by loading them onto a [DataLoader](https://fluxml.ai/Flux.jl/stable/data/dataloader/#Flux.Data.DataLoader) object.
-
-```julia
-function getdata(args)
- ENV["DATADEPS_ALWAYS_ACCEPT"] = "true"
-
- # Loading Dataset
- xtrain, ytrain = MLDatasets.MNIST.traindata(Float32)
- xtest, ytest = MLDatasets.MNIST.testdata(Float32)
-
- # Reshape Data in order to flatten each image into a linear array
- xtrain = Flux.flatten(xtrain)
- xtest = Flux.flatten(xtest)
-
- # One-hot-encode the labels
- ytrain, ytest = onehotbatch(ytrain, 0:9), onehotbatch(ytest, 0:9)
-
- # Batching
- train_data = DataLoader((xtrain, ytrain), batchsize=args.batchsize, shuffle=true)
- test_data = DataLoader((xtest, ytest), batchsize=args.batchsize)
-
- return train_data, test_data
-end
-```
-
-
-`getdata` performs the following steps:
-
-* **Loads MNIST data set:** Loads the train and test set tensors. The shape of train data is `28x28x60000` and test data is `28X28X10000`.
-* **Reshapes the train and test data:** Uses the [flatten](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.flatten) function to reshape the train data set into a `784x60000` array and test data set into a `784x10000`. Notice that we reshape the data so that we can pass these as arguments for the input layer of our model (a simple MLP expects a vector as an input).
-* **One-hot encodes the train and test labels:** Creates a batch of one-hot vectors so we can pass the labels of the data as arguments for the loss function. For this example, we use the [logitcrossentropy](https://fluxml.ai/Flux.jl/stable/models/losses/#Flux.Losses.logitcrossentropy) function and it expects data to be one-hot encoded.
-* **Creates batches of data:** Creates two DataLoader objects (train and test) that handle data mini-batches of size `1024 ` (as defined above). We create these two objects so that we can pass the entire data set through the loss function at once when training our model. Also, it shuffles the data points during each iteration (`shuffle=true`).
-
-## Model
-
-As we mentioned above, a MLP consist of *three* layers that are fully connected. For this example, we define out model with the following layers and dimensions:
-
-* **Input:** It has `784` perceptrons (the MNIST image size is `28x28`). We flatten the train and test data so that we can pass them as arguments to this layer.
-* **Hidden:** It has `32` perceptrons that use the [relu](https://fluxml.ai/Flux.jl/stable/models/nnlib/#NNlib.relu) activation function.
-* **Output:** It has `10` perceptrons that output the model's prediction or probability that a digit is 0 to 9.
-
-
-We define our model with the `build_model` function:
-
-```julia
-function build_model(; imgsize=(28,28,1), nclasses=10)
- return Chain(
- Dense(prod(imgsize), 32, relu),
- Dense(32, nclasses))
-end
-```
-
-
-Note that we use the functions [Dense](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.Dense) so that our model is *densely* (or fully) connected and [Chain](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.Chain) to chain the computation of the three layers.
-
-## Loss functions
-
-Now, we define the loss function `loss_all`. It expects a DataLoader object and the `model` function we defined aboved as arguments. Notice that this function iterates through the `dataloader` object in mini-batches and uses the function [logitcrossentropy](https://fluxml.ai/Flux.jl/stable/models/losses/#Flux.Losses.logitcrossentropy) to compute the difference between the predicted and actual values.
-
-```julia
-function loss_all(dataloader, model)
- l = 0f0
- for (x,y) in dataloader
- l += logitcrossentropy(model(x), y)
- end
- l/length(dataloader)
-end
-```
-
-
-In addition, we define the function (`accuracy`) to report the accuracy of our model during the training process. To compute the accuray, we need to decode the output of our model using the [onecold](https://fluxml.ai/Flux.jl/stable/data/onehot/#Flux.onecold) function.
-
-```julia
-function accuracy(data_loader, model)
- acc = 0
- for (x,y) in data_loader
- acc += sum(onecold(cpu(model(x))) .== onecold(cpu(y)))*1 / size(x,2)
- end
- acc/length(data_loader)
-end
-```
-
-
-## Train our model
-
-Finally, we create the `train` function that calls the functions we defined and trains the model.
-
-```julia
-function train(; kws...)
- # Initializing Model parameters
- args = Args(; kws...)
-
- # Load Data
- train_data,test_data = getdata(args)
-
- # Construct model
- m = build_model()
- train_data = args.device.(train_data)
- test_data = args.device.(test_data)
- m = args.device(m)
- loss(x,y) = logitcrossentropy(m(x), y)
-
- ## Training
- evalcb = () -> @show(loss_all(train_data, m))
- opt = ADAM(args.η)
-
- @epochs args.epochs Flux.train!(loss, params(m), train_data, opt, cb = evalcb)
-
- @show accuracy(train_data, m)
-
- @show accuracy(test_data, m)
-end
-```
-
-
-`train` performs the following steps:
-
-* **Initializes the model parameters:** Creates the `args` object that contains the defult values for training our model.
-* **Loads the train and test data:** Calls the function `getdata` we defined above.
-* **Constructs the model:** Builds the model and loads the train and test data sets, and our model onto the GPU (if available).
-* **Trains the model:** Defines the *callback* function `evalcb` to show the value of the `loss_all` function during the training process. Then, it sets [ADAM](https://fluxml.ai/Flux.jl/stable/training/optimisers/#Flux.Optimise.ADAM) as the optimiser for training out model. Finally, it runs the training process with the macro `@epochs` for `10` epochs (as defined in the `args` object) and shows the `accuracy` value for the train and test data.
-
-
-To see the full version of this example, see [Simple multi-layer perceptron - model-zoo](https://github.com/FluxML/model-zoo/blob/master/vision/mlp_mnist/mlp_mnist.jl).
-
-## Resources
-
-* [3Blue1Brown Neural networks videos](https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi).
-* [Neural Networks and Deep Learning](http://neuralnetworksanddeeplearning.com/).
diff --git a/tutorialposts/2021-02-07-convnet.md b/tutorialposts/2021-02-07-convnet.md
deleted file mode 100644
index f13ba112..00000000
--- a/tutorialposts/2021-02-07-convnet.md
+++ /dev/null
@@ -1,261 +0,0 @@
-+++
-title = "Simple ConvNet"
-published = "7 February 2021"
-author = "Elliot Saba, Adarsh Kumar, Mike J Innes, Dhairya Gandhi, Sudhanshu Agrawal, Sambit Kumar Dash, fps.io, Carlo Lucibello, Andrew Dinhobl, Liliana Badillo"
-+++
-
-In this tutorial, we build a simple Convolutional Neural Network (ConvNet) to classify the MNIST dataset. This model has a simple architecture with three feature detection layers (Conv -> ReLU -> MaxPool) followed by a final dense layer that classifies MNIST handwritten digits. Note that this model, while simple, should hit around 99% test accuracy after training for approximately 20 epochs.
-
-This example writes out the saved model to the file `mnist_conv.bson`. Also, it demonstrates basic model construction, training, saving, conditional early-exit, and learning rate scheduling.
-
-To run this example, we need the following packages:
-
-```julia
-using Flux, MLDatasets, Statistics
-using Flux: onehotbatch, onecold, logitcrossentropy
-using MLDatasets: MNIST
-using Base.Iterators: partition
-using Printf, BSON
-using Parameters: @with_kw
-using CUDA
-CUDA.allowscalar(false)
-```
-
-We set default values for learning rate, batch size, number of epochs, and path for saving the file `mnist_conv.bson`:
-
-```julia
-@with_kw mutable struct Args
- lr::Float64 = 3e-3
- epochs::Int = 20
- batch_size = 128
- savepath::String = "./"
-end
-```
-
-To train our model, we need to bundle images together with their labels and group them into mini-batches (makes the training process faster). We define the function `make_minibatch` that takes as inputs the images (`X`) and their labels (`Y`) as well as the indices for the mini-batches (`idx`):
-
-```julia
-function make_minibatch(X, Y, idxs)
- X_batch = Array{Float32}(undef, size(X)[1:end-1]..., 1, length(idxs))
- for i in 1:length(idxs)
- X_batch[:, :, :, i] = Float32.(X[:,:,idxs[i]])
- end
- Y_batch = onehotbatch(Y[idxs], 0:9)
- return (X_batch, Y_batch)
-end
-```
-
-`make_minibatch` takes the following steps:
-
-* Creates the `X_batch` array of size `28x28x1x128` to store the mini-batches.
-* Stores the mini-batches in `X_batch`.
-* One hot encodes the labels of the images.
-* Stores the labels in `Y_batch`.
-
-
-
- `get_processed_data` loads the train and test data from `Flux.Data.MNIST`. First, it loads the images and labels of the train data set, and creates an array that contains the indices of the train images that correspond to each mini-batch (of size `args.batch_size`). Then, it calls the `make_minibatch` function to create all of the train mini-batches. Finally, it loads the test images and creates one mini-batch that contains them all.
-
-```julia
-function get_processed_data(args)
- # Load labels and images
- train_imgs, train_labels = MNIST.traindata()
- mb_idxs = partition(1:length(train_labels), args.batch_size)
- train_set = [make_minibatch(train_imgs, train_labels, i) for i in mb_idxs]
-
- # Prepare test set as one giant minibatch:
- test_imgs, test_labels = MNIST.testdata()
- test_set = make_minibatch(test_imgs, test_labels, 1:length(test_labels))
-
- return train_set, test_set
-
-end
-```
-
-
-Now, we define the `build_model` function that creates a ConvNet model which is composed of *three* convolution layers (feature detection) and *one* classification layer. The input layer size is `28x28`. The images are grayscale, which means there is only *one* channel (compared to 3 for RGB) in every data point. Combined together, the convolutional layer structure would look like `Conv(kernel, input_channels => output_channels, ...)`. Each convolution layer reduces the size of the image by applying the Rectified Linear unit (ReLU) and MaxPool operations.
-On the other hand, the classification layer outputs a vector of 10 dimensions (a dense layer), that is, the number of classes that the model will be able to predict.
-
-
-```julia
-function build_model(args; imgsize = (28,28,1), nclasses = 10)
- cnn_output_size = Int.(floor.([imgsize[1]/8,imgsize[2]/8,32]))
-
- return Chain(
- # First convolution, operating upon a 28x28 image
- Conv((3, 3), imgsize[3]=>16, pad=(1,1), relu),
- MaxPool((2,2)),
-
- # Second convolution, operating upon a 14x14 image
- Conv((3, 3), 16=>32, pad=(1,1), relu),
- MaxPool((2,2)),
-
- # Third convolution, operating upon a 7x7 image
- Conv((3, 3), 32=>32, pad=(1,1), relu),
- MaxPool((2,2)),
-
- # Reshape 3d array into a 2d one using `Flux.flatten`, at this point it should be (3, 3, 32, N)
- flatten,
- Dense(prod(cnn_output_size), 10))
-end
-```
-
-To chain the layers of a model we use the Flux function [Chain](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.Chain). It enables us to call the layers in sequence on a given input. Also, we use the function [flatten](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.flatten) to reshape the output image from the last convolution layer. Finally, we call the [Dense](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.Dense) function to create the classification layer.
-
-
-Before training our model, we need to define a few functions that will be helpful for the process:
-
-
-* `augment` augments the data by adding gaussian random noise to our image to make it more robust:
-
- ```julia
- augment(x) = x .+ gpu(0.1f0*randn(eltype(x), size(x)))
- ```
-
-
-* `anynan` checks whether any element of the params is NaN or not:
-
- ```julia
- anynan(x) = any(y -> any(isnan, y), x)
- ```
-
-* `accuracy` computes the accuracy of our ConvNet:
-
- ```julia
- accuracy(x, y, model) = mean(onecold(cpu(model(x))) .== onecold(cpu(y)))
- ```
-
-Finally, we define the `train` function:
-
-```julia
-function train(; kws...)
- args = Args(; kws...)
-
- @info("Loading data set")
- train_set, test_set = get_processed_data(args)
-
- # Define our model. We will use a simple convolutional architecture with
- # three iterations of Conv -> ReLU -> MaxPool, followed by a final Dense layer.
- @info("Building model...")
- model = build_model(args)
-
- # Load model and datasets onto GPU, if enabled
- train_set = gpu.(train_set)
- test_set = gpu.(test_set)
- model = gpu(model)
-
- # Make sure our model is nicely precompiled before starting our training loop
- model(train_set[1][1])
-
- # `loss()` calculates the crossentropy loss between our prediction `y_hat`
- # (calculated from `model(x)`) and the ground truth `y`. We augment the data
- # a bit, adding gaussian random noise to our image to make it more robust.
- function loss(x, y)
- x̂ = augment(x)
- ŷ = model(x̂)
- return logitcrossentropy(ŷ, y)
- end
-
- # Train our model with the given training set using the ADAM optimizer and
- # printing out performance against the test set as we go.
- opt = ADAM(args.lr)
-
- @info("Beginning training loop...")
- best_acc = 0.0
- last_improvement = 0
- for epoch_idx in 1:args.epochs
- # Train for a single epoch
- Flux.train!(loss, params(model), train_set, opt)
-
- # Terminate on NaN
- if anynan(Flux.params(model))
- @error "NaN params"
- break
- end
-
- # Calculate accuracy:
- acc = accuracy(test_set..., model)
-
- @info(@sprintf("[%d]: Test accuracy: %.4f", epoch_idx, acc))
- # If our accuracy is good enough, quit out.
- if acc >= 0.999
- @info(" -> Early-exiting: We reached our target accuracy of 99.9%")
- break
- end
-
- # If this is the best accuracy we've seen so far, save the model out
- if acc >= best_acc
- @info(" -> New best accuracy! Saving model out to mnist_conv.bson")
- BSON.@save joinpath(args.savepath, "mnist_conv.bson") params=cpu.(params(model)) epoch_idx acc
- best_acc = acc
- last_improvement = epoch_idx
- end
-
- # If we haven't seen improvement in 5 epochs, drop our learning rate:
- if epoch_idx - last_improvement >= 5 && opt.eta > 1e-6
- opt.eta /= 10.0
- @warn(" -> Haven't improved in a while, dropping learning rate to $(opt.eta)!")
-
- # After dropping learning rate, give it a few epochs to improve
- last_improvement = epoch_idx
- end
-
- if epoch_idx - last_improvement >= 10
- @warn(" -> We're calling this converged.")
- break
- end
- end
-end
-```
-
-`train` calls the functions we defined above and trains our model. It stops when the model achieves 99% accuracy (early-exiting) or after performing 20 steps. More specifically, it performs the following steps:
-
- * Loads the MNIST dataset.
- * Builds our ConvNet model (as described above).
- * Loads the train and test data sets as well as our model onto a GPU (if available).
- * Defines a `loss` function that calculates the crossentropy between our prediction and the ground truth.
- * Sets the [ADAM optimiser](https://fluxml.ai/Flux.jl/stable/training/optimisers/#Flux.Optimise.ADAM) to train the model with learning rate `args.lr`.
- * Runs the training loop. For each step (or epoch), it executes the following:
- * Calls `Flux.train!` function to execute one training step.
- * If any of the parameters of our model is `NaN`, then the training process is terminated.
- * Calculates the model accuracy.
- * If the model accuracy is >= 0.999, then early-exiting is executed.
- * If the actual accuracy is the best so far, then the model is saved to `mnist_conv.bson`. Also, the new best accuracy and the current epoch is saved.
- * If there has not been any improvement for the last 5 epochs, then the learning rate is dropped and the process waits a little longer for the accuracy to improve.
- * If the last improvement was more than 10 epochs ago, then the process is terminated.
-
-
-Finally, to test our model we define the `test` function:
-
-```julia
-function test(; kws...)
- args = Args(; kws...)
-
- # Loading the test data
- _,test_set = get_processed_data(args)
-
- # Re-constructing the model with random initial weights
- model = build_model(args)
-
- # Loading the saved parameters
- BSON.@load joinpath(args.savepath, "mnist_conv.bson") params
-
- # Loading parameters onto the model
- Flux.loadparams!(model, params)
-
- test_set = gpu.(test_set)
- model = gpu(model)
- @show accuracy(test_set...,model)
-end
-```
-
-`test` loads the MNIST test data set, reconstructs the model, and loads the saved parameters (in `mnist_conv.bson`) onto it. Finally, it computes our model's predictions for the test set and shows the test accuracy (around 99%).
-
-To see the full version of this example, see [Simple ConvNets - model-zoo](https://github.com/FluxML/model-zoo/blob/master/vision/conv_mnist/conv_mnist.jl).
-
-## Resources
-
-* [Neural Networks in Flux.jl with Huda Nassar (working with the MNIST dataset)](https://youtu.be/Oxi0Pfmskus)
-* [Convolutional Neural Networks (CNNs / ConvNets)](https://cs231n.github.io/convolutional-networks/).
-* [Convolutional Neural Networks Tutorial in PyTorch](https://adventuresinmachinelearning.com/convolutional-neural-networks-tutorial-in-pytorch/).
-
diff --git a/tutorialposts/2021-10-08-dcgan-mnist.md b/tutorialposts/2021-10-08-dcgan-mnist.md
deleted file mode 100644
index 4d339113..00000000
--- a/tutorialposts/2021-10-08-dcgan-mnist.md
+++ /dev/null
@@ -1,369 +0,0 @@
-+++
-title = "Deep Convolutional Generative Adversarial Network (DCGAN)"
-published = "8 October 2021"
-author = "Deeptendu Santra"
-+++
-
-This is a beginner level tutorial for generating images of handwritten digits using a [Deep Convolutional Generative Adversarial Network](https://arxiv.org/pdf/1511.06434.pdf) inspired by the [TensorFlow tutorial on DCGAN](https://www.tensorflow.org/tutorials/generative/dcgan).
-
-## What are GANs?
-[Generative Adversarial Neural Networks or simply GANs](https://arxiv.org/abs/1406.2661) introduced by Goodfellow et al. is one of the most innovative ideas in modern-day machine learning. GANs are used extensively in the field of image and audio processing to generate high-quality synthetic data that can easily be passed off as real data.
-
-A GAN is composed of two sub-models - the **generator** and the **discriminator** acting against one another. The generator can be considered as an artist who draws (generates) new images that look real, whereas the discriminator is a critic who learns to tell real images apart from fakes.
-
-
-
-The GAN starts with a generator and discriminator which have very little or no idea about the underlying data. During training, the generator progressively becomes better at creating images that look real, while the discriminator becomes better at telling them apart. The process reaches equilibrium when the discriminator can no longer distinguish real images from fakes.
-
-
-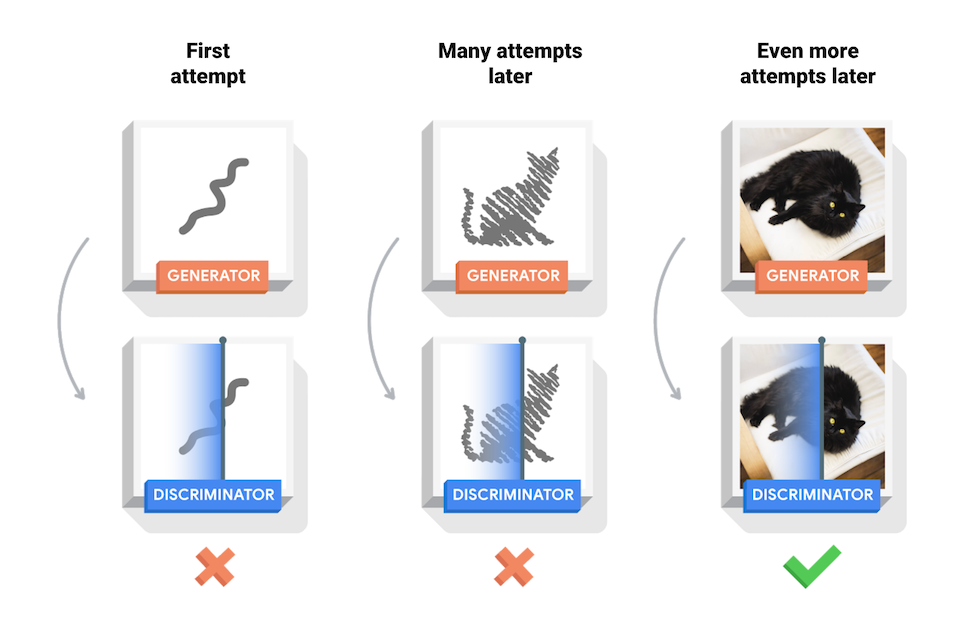
-
-[[source]](https://www.tensorflow.org/tutorials/generative/dcgan)
-
-This tutorial demonstrates the process of training a DC-GAN on the [MNIST dataset for handwritten digits](http://yann.lecun.com/exdb/mnist/). The following animation shows a series of images produced by the generator as it was trained for 25 epochs. The images begin as random noise, but over time, the images become increasingly similar to handwritten numbers.
-
-~~~
-
-
-
-
-~~~
-
-## Setup
-
-We need to install some Julia packages before we start with our implementation of DCGAN.
-
-```julia
-using Pkg
-
-# Activate a new project environment in the current directory
-Pkg.activate(".")
-# Add the required packages to the environment
-Pkg.add(["Images", "Flux", "MLDatasets", "CUDA", "Parameters"])
-```
-*Note: Depending on your internet speed, it may take a few minutes for the packages install.*
-
-
-After installing the libraries, load the required packages and functions:
-```julia
-using Base.Iterators: partition
-using Printf
-using Statistics
-using Random
-using Images
-using Parameters: @with_kw
-using Flux
-using Flux.Data: DataLoader
-using Flux.Optimise: update!
-using Flux.Losses: logitbinarycrossentropy
-using MLDatasets: MNIST
-using CUDA
-```
-
-Now we set default values for the learning rates, batch size, epochs, the usage of a GPU (if available) and other hyperparameters for our model.
-
-```julia
-@with_kw struct HyperParams
- batch_size::Int = 128
- latent_dim::Int = 100
- epochs::Int = 25
- verbose_freq::Int = 1000
- output_dim::Int = 5
- disc_lr::Float64 = 0.0002
- gen_lr::Float64 = 0.0002
- device::Function = gpu
-end
-```
-
-## Loading the data
-As mentioned before, we will be using the MNIST dataset for handwritten digits. So we begin with a simple function for loading and pre-processing the MNIST images:
-```julia
-function load_MNIST_images(hparams)
- images = MNIST.traintensor(Float32)
-
- # Normalize the images to (-1, 1)
- normalized_images = @. 2f0 * images - 1f0
- image_tensor = reshape(normalized_images, 28, 28, 1, :)
-
- # Create a dataloader that iterates over mini-batches of the image tensor
- dataloader = DataLoader(image_tensor, batchsize=hparams.batch_size, shuffle=true)
-
- return dataloader
-end
-```
-To learn more about loading images in Flux, you can check out [this tutorial](https://fluxml.ai/tutorials/2021/01/21/data-loader.html).
-
-*Note: The data returned from the dataloader is loaded is on the CPU. To train on the GPU, we need to transfer the data to the GPU beforehand.*
-
-## Create the models
-
-
-### The generator
-
-Our generator, a.k.a. the artist, is a neural network that maps low dimensional data to a high dimensional form.
-
-- This low dimensional data (seed) is generally a vector of random values sampled from a normal distribution.
-- The high dimensional data is the generated image.
-
-The `Dense` layer is used for taking the seed as an input which is upsampled several times using the [ConvTranspose](https://fluxml.ai/Flux.jl/stable/models/layers/#Flux.ConvTranspose) layer until we reach the desired output size (in our case, 28x28x1). Furthermore, after each `ConvTranspose` layer, we apply the Batch Normalization to stabilize the learning process.
-
-We will be using the [relu](https://fluxml.ai/Flux.jl/stable/models/nnlib/#NNlib.relu) activation function for each layer except the output layer, where we use `tanh` activation.
-
-We will also apply the weight initialization method mentioned in the original DCGAN paper.
-
-```julia
-# Function for intializing the model weights with values
-# sampled from a Gaussian distribution with μ=0 and σ=0.02
-dcgan_init(shape...) = randn(Float32, shape) * 0.02f0
-```
-
-
-```julia
-function Generator(latent_dim)
- Chain(
- Dense(latent_dim, 7*7*256, bias=false),
- BatchNorm(7*7*256, relu),
-
- x -> reshape(x, 7, 7, 256, :),
-
- ConvTranspose((5, 5), 256 => 128; stride = 1, pad = 2, init = dcgan_init, bias=false),
- BatchNorm(128, relu),
-
- ConvTranspose((4, 4), 128 => 64; stride = 2, pad = 1, init = dcgan_init, bias=false),
- BatchNorm(64, relu),
-
- # The tanh activation ensures that output is in range of (-1, 1)
- ConvTranspose((4, 4), 64 => 1, tanh; stride = 2, pad = 1, init = dcgan_init, bias=false),
- )
-end
-```
-
-Time for a small test!! We create a dummy generator and feed a random vector as a seed to the generator. If our generator is initialized correctly it will return an array of size (28, 28, 1, `batch_size`). The `@assert` macro in Julia will raise an exception for the wrong output size.
-
-```julia
-# Create a dummy generator of latent dim 100
-generator = Generator(100)
-noise = randn(Float32, 100, 3) # The last axis is the batch size
-
-# Feed the random noise to the generator
-gen_image = generator(noise)
-@assert size(gen_image) == (28, 28, 1, 3)
-```
-
-
-Our generator model is yet to learn the correct weights, so it does not produce a recognizable image for now. To train our poor generator we need its equal rival, the *discriminator*.
-
-
-
-### Discriminator
-
-The Discriminator is a simple CNN based image classifier. The `Conv` layer a is used with a [leakyrelu](https://fluxml.ai/Flux.jl/stable/models/nnlib/#NNlib.leakyrelu) activation function.
-
-```julia
-function Discriminator()
- Chain(
- Conv((4, 4), 1 => 64; stride = 2, pad = 1, init = dcgan_init),
- x->leakyrelu.(x, 0.2f0),
- Dropout(0.3),
-
- Conv((4, 4), 64 => 128; stride = 2, pad = 1, init = dcgan_init),
- x->leakyrelu.(x, 0.2f0),
- Dropout(0.3),
-
- # The output is now of the shape (7, 7, 128, batch_size)
- flatten,
- Dense(7 * 7 * 128, 1)
- )
-end
-```
-For a more detailed implementation of a CNN-based image classifier, you can refer to [this tutorial](https://fluxml.ai/tutorials/2021/02/07/convnet.html).
-
-Now let us check if our discriminator is working:
-
-```julia
-# Dummy Discriminator
-discriminator = Discriminator()
-# We pass the generated image to the discriminator
-logits = discriminator(gen_image)
-@assert size(logits) == (1, 3)
-```
-
-Just like our dummy generator, the untrained discriminator has no idea about what is a real or fake image. It needs to be trained alongside the generator to output positive values for real images, and negative values for fake images.
-
-## Loss functions for GAN
-
-In a GAN problem, there are only two labels involved: fake and real. So Binary CrossEntropy is an easy choice for a preliminary loss function.
-
-But even if Flux's `binarycrossentropy` does the job for us, due to numerical stability it is always preferred to compute cross-entropy using logits. Flux provides [logitbinarycrossentropy](https://fluxml.ai/Flux.jl/stable/models/losses/#Flux.Losses.logitbinarycrossentropy) specifically for this purpose. Mathematically it is equivalent to `binarycrossentropy(σ(ŷ), y, kwargs...).`
-
-
-### Discriminator Loss
-
-The discriminator loss quantifies how well the discriminator can distinguish real images from fakes. It compares
-
-- discriminator's predictions on real images to an array of 1s, and
-- discriminator's predictions on fake (generated) images to an array of 0s.
-
-These two losses are summed together to give a scalar loss. So we can write the loss function of the discriminator as:
-
-```julia
-function discriminator_loss(real_output, fake_output)
- real_loss = logitbinarycrossentropy(real_output, 1)
- fake_loss = logitbinarycrossentropy(fake_output, 0)
- return real_loss + fake_loss
-end
-```
-
-### Generator Loss
-
-The generator's loss quantifies how well it was able to trick the discriminator. Intuitively, if the generator is performing well, the discriminator will classify the fake images as real (or 1).
-
-```julia
-generator_loss(fake_output) = logitbinarycrossentropy(fake_output, 1)
-```
-
-We also need optimizers for our network. Why you may ask? Read more [here](https://towardsdatascience.com/overview-of-various-optimizers-in-neural-networks-17c1be2df6d5). For both the generator and discriminator, we will use the [ADAM optimizer](https://fluxml.ai/Flux.jl/stable/training/optimisers/#Flux.Optimise.ADAM).
-
-## Utility functions
-
-The output of the generator ranges from (-1, 1), so it needs to be de-normalized before we can display it as an image. To make things a bit easier, we define a function to visualize the output of the generator as a grid of images.
-
-```julia
-function create_output_image(gen, fixed_noise, hparams)
- fake_images = cpu(gen.(fixed_noise))
- image_array = reduce(vcat, reduce.(hcat, partition(fake_images, hparams.output_dim)))
- image_array = permutedims(dropdims(image_array; dims=(3, 4)), (2, 1))
- image_array = @. Gray(image_array + 1f0) / 2f0
- return image_array
-end
-```
-
-## Training
-
-For the sake of simplifying our training problem, we will divide the generator and discriminator training into two separate functions.
-
-```julia
-function train_discriminator!(gen, disc, real_img, fake_img, opt, ps, hparams)
-
- disc_loss, grads = Flux.withgradient(ps) do
- discriminator_loss(disc(real_img), disc(fake_img))
- end
-
- # Update the discriminator parameters
- update!(opt, ps, grads)
- return disc_loss
-end
-```
-
-We define a similar function for the generator.
-
-```julia
-function train_generator!(gen, disc, fake_img, opt, ps, hparams)
-
- gen_loss, grads = Flux.withgradient(ps) do
- generator_loss(disc(fake_img))
- end
-
- update!(opt, ps, grads)
- return gen_loss
-end
-```
-
-
-Now that we have defined every function we need, we integrate everything into a single `train` function where we first set up all the models and optimizers and then train the GAN for a specified number of epochs.
-
-```julia
-function train(hparams)
-
- dev = hparams.device
- # Check if CUDA is actually present
- if hparams.device == gpu
- if !CUDA.has_cuda()
- dev = cpu
- @warn "No gpu found, falling back to CPU"
- end
- end
-
- # Load the normalized MNIST images
- dataloader = load_MNIST_images(hparams)
-
- # Initialize the models and pass them to correct device
- disc = Discriminator() |> dev
- gen = Generator(hparams.latent_dim) |> dev
-
- # Collect the generator and discriminator parameters
- disc_ps = params(disc)
- gen_ps = params(gen)
-
- # Initialize the ADAM optimizers for both the sub-models
- # with respective learning rates
- disc_opt = ADAM(hparams.disc_lr)
- gen_opt = ADAM(hparams.gen_lr)
-
- # Create a batch of fixed noise for visualizing the training of generator over time
- fixed_noise = [randn(Float32, hparams.latent_dim, 1) |> dev for _=1:hparams.output_dim^2]
-
- # Training loop
- train_steps = 0
- for ep in 1:hparams.epochs
- @info "Epoch $ep"
- for real_img in dataloader
-
- # Transfer the data to the GPU
- real_img = real_img |> dev
-
- # Create a random noise
- noise = randn!(similar(real_img, (hparams.latent_dim, hparams.batch_size)))
- # Pass the noise to the generator to create a fake imagae
- fake_img = gen(noise)
-
- # Update discriminator and generator
- loss_disc = train_discriminator!(gen, disc, real_img, fake_img, disc_opt, disc_ps, hparams)
- loss_gen = train_generator!(gen, disc, fake_img, gen_opt, gen_ps, hparams)
-
- if train_steps % hparams.verbose_freq == 0
- @info("Train step $(train_steps), Discriminator loss = $(loss_disc), Generator loss = $(loss_gen)")
- # Save generated fake image
- output_image = create_output_image(gen, fixed_noise, hparams)
- save(@sprintf("output/dcgan_steps_%06d.png", train_steps), output_image)
- end
- train_steps += 1
- end
- end
-
- output_image = create_output_image(gen, fixed_noise, hparams)
- save(@sprintf("output/dcgan_steps_%06d.png", train_steps), output_image)
-
- return nothing
-end
-```
-
-Now we finally get to train the GAN:
-
-```julia
-# Define the hyper-parameters (here, we go with the default ones)
-hparams = HyperParams()
-train(hparams)
-```
-
-## Output
-The generated images are stored inside the `output` folder. To visualize the output of the generator over time, we create a gif of the generated images.
-
-```julia
-folder = "output"
-# Get the image filenames from the folder
-img_paths = readdir(folder, join=true)
-# Load all the images as an array
-images = load.(img_paths)
-# Join all the images in the array to create a matrix of images
-gif_mat = cat(images..., dims=3)
-save("./output.gif", gif_mat)
-```
-
-
-
-
-
-## Resources & References
-- [The DCGAN implementation in Model Zoo.](http=s://github.com/FluxML/model-zoo/blob/master/vision/dcgan_mnist/dcgan_mnist.jl)
-
diff --git a/tutorialposts/2021-10-14-vanilla-gan.md b/tutorialposts/2021-10-14-vanilla-gan.md
deleted file mode 100644
index eb3ecce3..00000000
--- a/tutorialposts/2021-10-14-vanilla-gan.md
+++ /dev/null
@@ -1,283 +0,0 @@
-+++
-title = "Generative Adversarial Networks"
-published = "14 October 2021"
-author = "Ralph Kube"
-+++
-
-This tutorial describes how to implement a vanilla Generative Adversarial
-Network using Flux and how train it on the MNIST dataset. It is based on this
-[Pytorch tutorial](https://medium.com/ai-society/gans-from-scratch-1-a-deep-introduction-with-code-in-pytorch-and-tensorflow-cb03cdcdba0f). The original GAN [paper](https://arxiv.org/abs/1406.2661) by Goodfellow et al. is a great resource that describes the motivation and theory behind GANs:
-
-```
-In the proposed adversarial nets framework, the generative model is pitted against an adversary: a
-discriminative model that learns to determine whether a sample is from the model distribution or the
-data distribution. The generative model can be thought of as analogous to a team of counterfeiters,
-trying to produce fake currency and use it without detection, while the discriminative model is
-analogous to the police, trying to detect the counterfeit currency. Competition in this game drives
-both teams to improve their methods until the counterfeits are indistinguishable from the genuine
-articles.
-```
-
-Let's implement a GAN in Flux. To get started we first import a few useful packages:
-
-
-```julia
-using MLDatasets: MNIST
-using Flux.Data: DataLoader
-using Flux
-using CUDA
-using Zygote
-using UnicodePlots
-```
-
-To download a package in the Julia REPL, type `]` to enter package mode and then
-type `add MLDatasets` or perform this operation with the Pkg module like this
-
-```julia
-> import Pkg
-> Pkg.add(MLDatasets)
-```
-
-While [UnicodePlots]() is not necessary, it can be used to plot generated samples
-into the terminal during training. Having direct feedback, instead of looking
-at plots in a separate window, use fantastic for debugging.
-
-
-Next, let us define values for learning rate, batch size, epochs, and other
-hyper-parameters. While we are at it, we also define optimizers for the generator
-and discriminator network. More on what these are later.
-
-```julia
- lr_g = 2e-4 # Learning rate of the generator network
- lr_d = 2e-4 # Learning rate of the discriminator network
- batch_size = 128 # batch size
- num_epochs = 1000 # Number of epochs to train for
- output_period = 100 # Period length for plots of generator samples
- n_features = 28 * 28# Number of pixels in each sample of the MNIST dataset
- latent_dim = 100 # Dimension of latent space
- opt_dscr = ADAM(lr_d)# Optimizer for the discriminator
- opt_gen = ADAM(lr_g) # Optimizer for the generator
-```
-
-
-In this tutorial I'm assuming that a CUDA-enabled GPU is available on the
-system where the script is running. If this is not the case, simply remove
-the `|>gpu` decorators: [piping](https://docs.julialang.org/en/v1/manual/functions/#Function-composition-and-piping).
-
-## Data loading
-The MNIST data set is available from [MLDatasets](https://juliaml.github.io/MLDatasets.jl/latest/). The first time you instantiate it you will be prompted
-if you want to download it. You should agree to this.
-
-GANs can be trained unsupervised. Therefore only keep the images from the training
-set and discard the labels.
-
-After we load the training data we re-scale the data from values in [0:1]
-to values in [-1:1]. GANs are notoriously tricky to train and this re-scaling
-is a recommended [GAN hack](https://github.com/soumith/ganhacks). The
-re-scaled data is used to define a data loader which handles batching
-and shuffling the data.
-
-```julia
- # Load the dataset
- train_x, _ = MNIST.traindata(Float32);
- # This dataset has pixel values ∈ [0:1]. Map these to [-1:1]
- train_x = 2f0 * reshape(train_x, 28, 28, 1, :) .- 1f0 |>gpu;
- # DataLoader allows to access data batch-wise and handles shuffling.
- train_loader = DataLoader(train_x, batchsize=batch_size, shuffle=true);
-```
-
-
-## Defining the Networks
-
-
-A vanilla GAN, the discriminator and the generator are both plain, [feed-forward
-multilayer perceptrons](https://boostedml.com/2020/04/feedforward-neural-networks-and-multilayer-perceptrons.html). We use leaky rectified linear units [leakyrelu](https://fluxml.ai/Flux.jl/stable/models/nnlib/#NNlib.leakyrelu) to ensure out model is non-linear.
-
-Here, the coefficient `α` (in the `leakyrelu` below), is set to 0.2. Empirically,
-this value allows for good training of the network (based on prior experiments).
-It has also been found that Dropout ensures a good generalization of the learned
-network, so we will use that below. Dropout is usually active when training a
-model and inactive in inference. Flux automatically sets the training mode when
-calling the model in a gradient context. As a final non-linearity, we use the
-`sigmoid` activation function.
-
-```julia
-discriminator = Chain(Dense(n_features, 1024, x -> leakyrelu(x, 0.2f0)),
- Dropout(0.3),
- Dense(1024, 512, x -> leakyrelu(x, 0.2f0)),
- Dropout(0.3),
- Dense(512, 256, x -> leakyrelu(x, 0.2f0)),
- Dropout(0.3),
- Dense(256, 1, sigmoid)) |> gpu
-```
-
-Let's define the generator in a similar fashion. This network maps a latent
-variable (a variable that is not directly observed but instead inferred) to the
-image space and we set the input and output dimension accordingly. A `tanh` squashes
-the output of the final layer to values in [-1:1], the same range that we squashed
-the training data onto.
-
-```julia
-generator = Chain(Dense(latent_dim, 256, x -> leakyrelu(x, 0.2f0)),
- Dense(256, 512, x -> leakyrelu(x, 0.2f0)),
- Dense(512, 1024, x -> leakyrelu(x, 0.2f0)),
- Dense(1024, n_features, tanh)) |> gpu
-```
-
-
-
-## Training functions for the networks
-
-To train the discriminator, we present it with real data from the MNIST
-data set and with fake data and reward it by predicting the correct labels for
-each sample. The correct labels are of course 1 for in-distribution data
-and 0 for out-of-distribution data coming from the generator.
-[Binary cross entropy](https://fluxml.ai/Flux.jl/stable/models/losses/#Flux.Losses.binarycrossentropy)
-is the loss function of choice. While the Flux documentation suggests to use
-[Logit binary cross entropy](https://fluxml.ai/Flux.jl/stable/models/losses/#Flux.Losses.logitcrossentropy),
-the GAN seems to be difficult to train with this loss function.
-This function returns the discriminator loss for logging purposes. We can
-calculate the loss in the same call as evaluating the pullback and resort
-to getting the pullback directly from Zygote instead of calling
-`Flux.train!` on the model. To calculate the gradients of the loss
-function with respect to the parameters of the discriminator we then only have to
-evaluate the pullback with a seed gradient of 1.0. These gradients are used
-to update the model parameters
-
-
-```julia
-function train_dscr!(discriminator, real_data, fake_data)
- this_batch = size(real_data)[end] # Number of samples in the batch
- # Concatenate real and fake data into one big vector
- all_data = hcat(real_data, fake_data)
-
- # Target vector for predictions: 1 for real data, 0 for fake data.
- all_target = [ones(eltype(real_data), 1, this_batch) zeros(eltype(fake_data), 1, this_batch)] |> gpu;
-
- ps = Flux.params(discriminator)
- loss, pullback = Zygote.pullback(ps) do
- preds = discriminator(all_data)
- loss = Flux.Losses.binarycrossentropy(preds, all_target)
- end
- # To get the gradients we evaluate the pullback with 1.0 as a seed gradient.
- grads = pullback(1f0)
-
- # Update the parameters of the discriminator with the gradients we calculated above
- Flux.update!(opt_dscr, Flux.params(discriminator), grads)
-
- return loss
-end
-```
-
-
-Now we need to define a function to train the generator network. The job of the
-generator is to fool the discriminator so we reward the generator when the discriminator
-predicts a high probability for its samples to be real data. In the training function
-we first need to sample some noise, i.e. normally distributed data. This has
-to be done outside the pullback since we don't want to get the gradients with
-respect to the noise, but to the generator parameters. Inside the pullback we need
-to first apply the generator to the noise since we will take the gradient with respect
-to the parameters of the generator. We also need to call the discriminator in order
-to evaluate the loss function inside the pullback. Here we need to remember to deactivate
-the dropout layers of the discriminator. We do this by setting the discriminator into
-test mode before the pullback. Immediately after the pullback we set it back into training
-mode. Then we evaluate the pullback, call it with a seed gradient of 1.0 as above, update the
-parameters of the generator network and return the loss.
-
-
-```julia
-function train_gen!(discriminator, generator)
- # Sample noise
- noise = randn(latent_dim, batch_size) |> gpu;
-
- # Define parameters and get the pullback
- ps = Flux.params(generator)
- # Set discriminator into test mode to disable dropout layers
- testmode!(discriminator)
- # Evaluate the loss function while calculating the pullback. We get the loss for free
- loss, back = Zygote.pullback(ps) do
- preds = discriminator(generator(noise));
- loss = Flux.Losses.binarycrossentropy(preds, 1.)
- end
- # Evaluate the pullback with a seed-gradient of 1.0 to get the gradients for
- # the parameters of the generator
- grads = back(1.0f0)
- Flux.update!(opt_gen, Flux.params(generator), grads)
- # Set discriminator back into automatic mode
- trainmode!(discriminator, mode=:auto)
- return loss
-end
-```
-
-## Training
-Now we are ready to train the GAN. In the training loop we keep track
-of the per-sample loss of the generator and the discriminator, where
-we use the batch loss returned by the two training functions defined above.
-In each epoch we iterate over the mini-batches given by the data loader.
-Only minimal data processing needs to be done before the training functions
-can be called.
-
-```julia
-lossvec_gen = zeros(num_epochs)
-lossvec_dscr = zeros(num_epochs)
-
-for n in 1:num_epochs
- loss_sum_gen = 0.0f0
- loss_sum_dscr = 0.0f0
-
- for x in train_loader
- # - Flatten the images from 28x28xbatchsize to 784xbatchsize
- real_data = flatten(x);
-
- # Train the discriminator
- noise = randn(latent_dim, size(x)[end]) |> gpu
- fake_data = generator(noise)
- loss_dscr = train_dscr!(discriminator, real_data, fake_data)
- loss_sum_dscr += loss_dscr
-
- # Train the generator
- loss_gen = train_gen!(discriminator, generator)
- loss_sum_gen += loss_gen
- end
-
- # Add the per-sample loss of the generator and discriminator
- lossvec_gen[n] = loss_sum_gen / size(train_x)[end]
- lossvec_dscr[n] = loss_sum_dscr / size(train_x)[end]
-
- if n % output_period == 0
- @show n
- noise = randn(latent_dim, 4) |> gpu;
- fake_data = reshape(generator(noise), 28, 4*28);
- p = heatmap(fake_data, colormap=:inferno)
- print(p)
- end
-end
-```
-
-For the hyper-parameters shown in this example, the generator produces useful
-images after about 1000 epochs. And after about 5000 epochs the result look
-indistinguishable from real MNIST data. Using a Nvidia V100 GPU on a 2.7
-GHz Power9 CPU with 32 hardware threads, training 100 epochs takes about 80
-seconds when using the GPU. The GPU utilization is between 30 and 40%.
-To observe the network more frequently during training you can for example set
-`output_period=20`. Training the GAN using the CPU takes about 10 minutes
-per epoch and is not recommended.
-
-## Results
-
-Below you can see what some of the images output may look like after different numbers of epochs.
-
-
-
-
-
-
-
-
-
-## Resources
-
-* [A collection of GANs in Flux](https://github.com/AdarshKumar712/FluxGAN)
-* [Wikipedia](https://en.wikipedia.org/wiki/Generative_adversarial_network)
-* [GAN hacks](https://github.com/soumith/ganhacks)
-
From 4d20f0be793d0bb2e80f2a62f6184188910e734d Mon Sep 17 00:00:00 2001
From: Michael Abbott <32575566+mcabbott@users.noreply.github.com>
Date: Sat, 26 Nov 2022 23:22:48 -0500
Subject: [PATCH 02/10] Delete getting_started.md
---
getting_started.md | 213 ---------------------------------------------
1 file changed, 213 deletions(-)
delete mode 100644 getting_started.md
diff --git a/getting_started.md b/getting_started.md
deleted file mode 100644
index c255f656..00000000
--- a/getting_started.md
+++ /dev/null
@@ -1,213 +0,0 @@
-+++
-title = "Getting Started"
-+++
-
-Welcome! This section contains information on how to create your first machine learning model using Flux.
-
-Flux is 100% pure-Julia stack and provides lightweight abstractions on top of Julia's native GPU and AD support. It makes the easy things easy while remaining fully hackable. Also, Flux has a next-generation Automatic Differentiation (AD) system [Zygote](https://github.com/FluxML/Zygote.jl).
-
-
-## Before you start
-
-Before you begin using Flux, you need to install Julia version 1.3 or later. For more information on installing Julia, see [Download Julia](https://julialang.org/downloads/).
-
-After installing Julia, you can install Flux by running the following command in the Julia REPL:
-
-```julia
-julia> ] add Flux
-```
-
-Alternatively, you can run the following:
-
-```julia
-julia> using Pkg; Pkg.add("Flux")
-```
-
-Flux provides GPU support. For more information on obtaining GPU support, see [CUDA.jl](https://github.com/JuliaGPU/CUDA.jl) and [Flux documentation on GPU support](https://fluxml.ai/Flux.jl/stable/gpu/).
-
-## Getting Help
-
-If you run into any issues on your journey learning Flux.jl, please post on Stack Overflow under the [Flux.jl tag](https://stackoverflow.com/questions/tagged/flux.jl) or ask a question on the [Julia Discourse under the Machine Learning domain](https://discourse.julialang.org/c/domain/ml/).
-
-## Create your first model
-
-In this tutorial, you'll create your first machine learning model using Flux. This is a simple linear regression model that attempts to recover a linear function by looking at noisy examples.
-
-### Step 1: Import Flux
-
-To import Flux add the following:
-
-```julia
-using Flux
-```
-
-### Step 2: Create the training data
-First, we'll write a function that generates our "true" data. We'll use to use Flux to recover `W_truth` and `b_truth` by looking only at examples of the `ground_truth` function.
-
-```julia
-W_truth = [1 2 3 4 5;
- 5 4 3 2 1]
-b_truth = [-1.0; -2.0]
-ground_truth(x) = W_truth*x .+ b_truth
-```
-
-Next, we generate our training data by passing random vectors into the ground truth function. We'll also add Gaussian noise using `randn()` so that it's not *too* easy for Flux to figure out the model.
-
-```julia
-x_train = [ 5 .* rand(5) for _ in 1:10_000 ]
-y_train = [ ground_truth(x) + 0.2 .* randn(2) for x in x_train ]
-```
-
-There are two important things to note in this example which differ from real
-machine learning problems:
- - Our variables are individual vectors, stored inside another vector. Usually,
- we would have a collection of N-dimensional arrays (N >= 2) as our data.
- - In a real learning scenario, we would not have access to our ground truth,
- only the training examples.
-
-### Step 3: Define your model
-
-Next, we define the model we want to use to learn the data. We'll use the same form that we used for our training data:
-
-```julia
-model(x) = W*x .+ b
-```
-
-We need to set the parameters of the model (`W` and `b`) to some initial values. It's fairly common to use random values, so we'll do that:
-
-```julia
-W = rand(2, 5)
-b = rand(2)
-```
-
-You can learn more about defining models in this video:
-
-~~~
-
-
-
-~~~
-
-### Step 4: Define a loss function
-
-A loss function evaluates a machine learning model's performance. In other words, it measures how far the model is from its target prediction. Flux lets you define your own custom loss function, or you can use one of the [Loss Functions](https://fluxml.ai/Flux.jl/stable/training/training/#Loss-Functions-1) that Flux provides.
-
-For this example, we'll define a loss function that measures the squared distance from the predicted output to the actual output:
-
-```julia
-function loss(x, y)
- ŷ = model(x)
- sum((y .- ŷ).^2)
-end
-```
-
-### Step 5: Set an optimiser
-
-You train a machine learning model by running an optimization algorithm (optimiser) that finds the best parameters (`W` and `b`). The best parameters for a model are the ones that achieve the best score of the `loss` function. Flux provides [Optimisers](https://fluxml.ai/Flux.jl/stable/training/optimisers/) that you can use to train a model.
-
-For this tutorial, we'll use a classic gradient descent optimiser with learning rate η = 0.01:
-
-```julia
-opt = Descent(0.01)
-```
-
-### Step 6: Train your model
-
-Training a model is the process of computing the gradients with respect to the parameters for each input in the data. At every step, the optimiser updates all of the parameters until it finds a good value for them. This process can be written as a loop: we iterate over the examples in `x_train` and `y_train` and update the model for each example.
-
-To indicate that we want all derivatives of `W` and `b`, we write `ps = Flux.params(W, b)`. This is a convenience function that Flux provides so that we don't have to explicitly list every gradient we want. Check out the section on [Taking Gradients](https://fluxml.ai/Flux.jl/stable/models/basics/#Taking-Gradients) if you want to learn more about how this works.
-
-We can now execute the training procedure for our model:
-
-```julia
-train_data = zip(x_train, y_train)
-ps = Flux.params(W, b)
-
-for (x,y) in train_data
- gs = Flux.gradient(ps) do
- loss(x,y)
- end
- Flux.Optimise.update!(opt, ps, gs)
-end
-```
-
-> **Note:** With this pattern, it is easy to add more complex learning routines that make use of control flow, distributed compute, scheduling optimisations, etc. Note that the pattern above is a simple Julia *for loop* but it could also be replaced with a *while loop*.
-
-While writing your own loop is powerful, sometimes you just want to do the simple thing without writing too much code. Flux lets you do this with [Flux.train!](https://fluxml.ai/Flux.jl/stable/training/training/#Training-1), which runs one training epoch over a dataset. `Flux.train!` computes gradients and updates model parameters for every sample or batch of samples. In our case, we could have replaced the above loop with the following statement:
-
-```julia
-Flux.train!(loss, Flux.params(W, b), train_data, opt)
-```
-
-For more ways to train a model in Flux, see [Training](https://fluxml.ai/Flux.jl/stable/training/training/#Training-1).
-
-### Step 7: Examine the Results
-
-The training loop we ran modified `W` and `b` to be closer to the values used to generate the training data (`W` and `b`). We can see how well we did by printing out the difference between the learned and actual matrices.
-
-```julia
-@show W
-@show maximum(abs, W .- W_truth)
-```
-
-Because the data and initialization are random, your results may vary slightly, but in most cases, the largest difference between the elements of learned and actual `W` matrix is no more than 4%.
-
-### Step 8: Run the script
-
-Finally, create a file with extension `.jl` with the code above in any IDE and run it as `julia name-of-your-file.jl `. You can use the [Julia VSCode extension](https://www.julia-vscode.org/) to edit and run Julia code. Alternatively, you can run Julia code on a Jupyter notebook (see [IJulia](https://github.com/JuliaLang/IJulia.jl)). Here is the full version of the code:
-
-```julia
-using Flux
-
-# Define the ground truth model. We aim to recover W_truth and b_truth using
-# only examples of ground_truth()
-W_truth = [1 2 3 4 5;
- 5 4 3 2 1]
-b_truth = [-1.0; -2.0]
-ground_truth(x) = W_truth*x .+ b_truth
-
-# Generate the ground truth training data as vectors-of-vectors
-x_train = [ 5 .* rand(5) for _ in 1:10_000 ]
-y_train = [ ground_truth(x) + 0.2 .* randn(2) for x in x_train ]
-
-# Define and initialize the model we want to train
-model(x) = W*x .+ b
-W = rand(2, 5)
-b = rand(2)
-
-# Define pieces we need to train: loss function, optimiser, examples, and params
-function loss(x, y)
- ŷ = model(x)
- sum((y .- ŷ).^2)
-end
-opt = Descent(0.01)
-train_data = zip(x_train, y_train)
-ps = Flux.params(W, b)
-
-# Execute a training epoch
-for (x,y) in train_data
- gs = gradient(ps) do
- loss(x,y)
- end
- Flux.Optimise.update!(opt, ps, gs)
-end
-
-# An alternate way to execute a training epoch
-# Flux.train!(loss, Flux.params(W, b), train_data, opt)
-
-# Print out how well we did
-@show W
-@show maximum(abs, W .- W_truth)
-```
-
-
-## What's next
-
-Congratulations! You have created and trained a model using Flux. Now, you can continue exploring Flux's capabilities:
-
-* [60-minute blitz tutorial](tutorials/2020/09/15/deep-learning-flux.html) is a quick intro to Flux loosely based on [PyTorch's tutorial](https://pytorch.org/tutorials/beginner/deep_learning_60min_blitz.html).
-* [Flux Model Zoo](https://github.com/FluxML/model-zoo) contains various demonstrations of Flux.
-* [JuliaAcademy](https://juliaacademy.com/) offers introductory courses to Julia and Flux.
-* [Flux's official documentation](https://fluxml.ai/Flux.jl/stable/).
-
-As you continue to progress through your Flux and Julia journey, please feel free to share it on [Twitter and tag us](https://twitter.com/FluxML), we would love to see what awesome things the #FluxML community is up to.
From 3c8d2d7f180e7aed6a4d551e8c5efe51ee7abbd4 Mon Sep 17 00:00:00 2001
From: Michael Abbott <32575566+mcabbott@users.noreply.github.com>
Date: Sat, 26 Nov 2022 23:23:37 -0500
Subject: [PATCH 03/10] Update navbar.html
---
_layout/navbar.html | 122 +++++++++-----------------------------------
1 file changed, 25 insertions(+), 97 deletions(-)
diff --git a/_layout/navbar.html b/_layout/navbar.html
index 1fd6898e..89f5bf5d 100644
--- a/_layout/navbar.html
+++ b/_layout/navbar.html
@@ -1,118 +1,46 @@