-
Notifications
You must be signed in to change notification settings - Fork 203
Removed the resets to INT_MAX in etc/tune.c
#453
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Conversation
|
TBH I had the impression for already a while that the tuning doesn't really do what it promises... until now I only suspected it, but check out yourself... I executed but I'm a bit surprised of a lot of the timing diagrams I've seen today... maybe just another case of "wer viel misst, misst viel Mist"!? |
|
So it's slower now, if I understand your graphic correctly and it's not even a small difference? But I still made no absolute timings with the benchmark in The problem is that the Comba multiplication has an upper limit, all of the faster ones have lower limits (besides FFT which has both, but that's not in here). There is also a steep jump at Comba's upper limit. That together with the cascading down of the T-C algorithms makes the behaviour a bit chaotic overall.
There's a very good chance that that is true ;-) But the original run I made with all the squaring functions having a 128 limbs cut-off as a result was a bit…uhm…suspicious, to say the least and the single thing that changed was the resetting. Why did I decide against resetting? All of our fast multiplication/squaring algorithms are recursive and call a lower (or equal) T-C/school/Comba algo chosen by I'll make some "pretty pictures" this evening with some curves of the absolute run times of the individual functions to get a rough overview. It might help. And if it doesn't help we can still put it on the strawberries ;-) |
729b5a0 to
dedbd25
Compare
|
I think you should do.profiling (e.g. using perf) to see the hot spots of the different implementations. In theory toom-2==karatsuba, right? Or is there some other structural difference in our implementation? These higher toom variants should interpolate in-between until FFT becomes faster finally? Are you seeing this for larger bitsizes? I have to admit I cannot read your plots (I only see a difference between school and something else). |
|
And furthermore we should try to lift the comba limit by using a larger W if needed (as a first step get rid of WARRAY somehow, #447). |
Yes. You need that really fast multiplication for Newton division, I tried it with the current LTM versions but the cut-off is so far out that I first thought to have made an error while porting it from my old fork. And then there is the question if LTM needs all of that in the first place.
Argh, I didn't make them safe, sorry for that!
Yes, that's the theory. And it would work. Normally. But LTM is not really "normal" in that sense ;-) I have no quick solution at hand besides putting a note in the documentation but will work at it. Especially by testing other architectures or a least LTM's other limb-sizes. If it is just my old machine I'll put a note in the documentation, if it is elsewhere too it gets interesting.
I thought there is a hard technical limit? |
I think such things should be generated. Only write the generator once. Also Karatsuba could be generated in the same way then.
So TC3 is as fast as TC2 (Karatsuba) even for small numbers and will get faster than TC2 for larger numbers?
I lifted the limit in #447 as an example. This is how things are done in tfm. And after lifiting the limit, both full width and smaller digits could be used. |
|
Me: Oh, nice, a free weekend! Time for working on the non-biz to-do lists! But back to the to-do lists: while working at the accessibility of the graphics for @minad I came to the conclusion that there must a fundamental logic flaw in
Well… But I don't give up that easily, I'll find a solution before I start drawing my pension! ;-)
Generating the function from Maths or from the PARI/GP code?
It seems so, yes. One of the reasons is COMBA. Without COMBA only TC3-squaring is as fast as TC2-squaring. (But TC3-multiplying is not that far off in that case). And because you are currently working at it, @minad , it would be nice, if COMBA has a programmatically changeable cut-off (because it might be able to replace Karatsuba if COMBA has no upper limit)? Oh, and before I forget it, the graphics: No COMBA: And one with squaring. Interesting is the part without Karatsuba and the values evaluated with resetting (5000, 5000, 125, 128) and without (5000, 5000, 166, 246). |
|
That whole mess is indeed caused by the Comba multiplication/squaring. i tried a couple of higher TC's (TC-6 to TC-9, the coefficients get too big with TC-10) and found that choosing coefficients that are powers of two alone make a siginifcant difference. But tweaking those is a lot of tedious manual work and more than can be shoveled in a single WE. So closing this PR for good with the hope to open a new one with properly constructed Toom-Cook algorithms. |

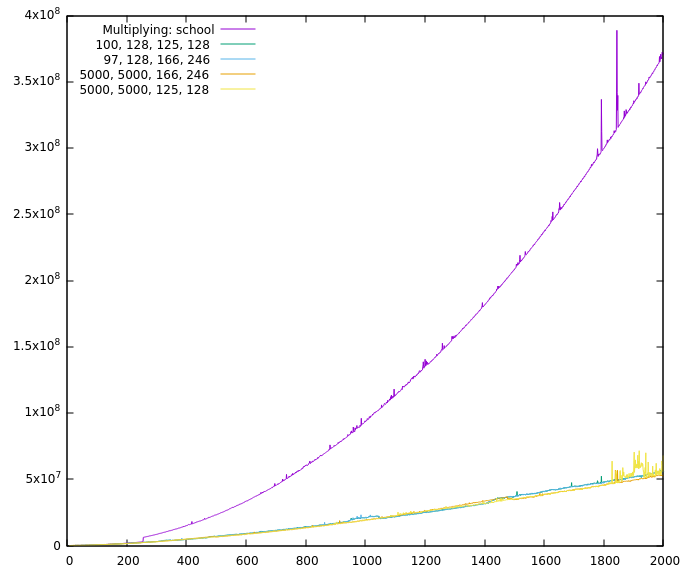
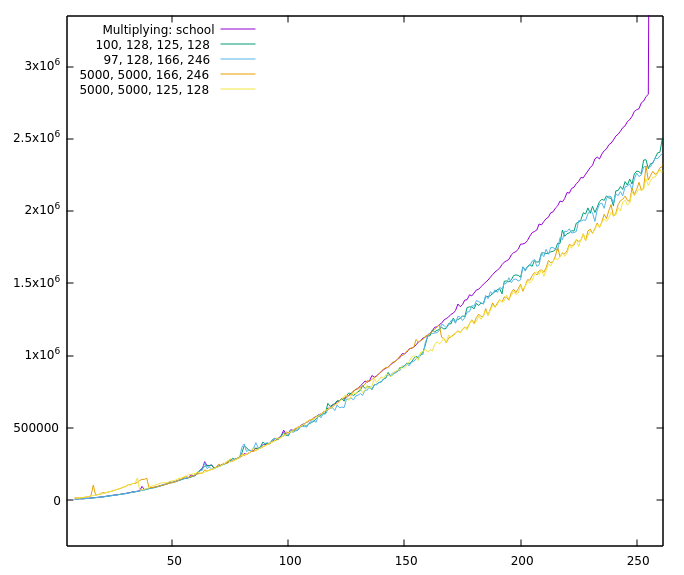
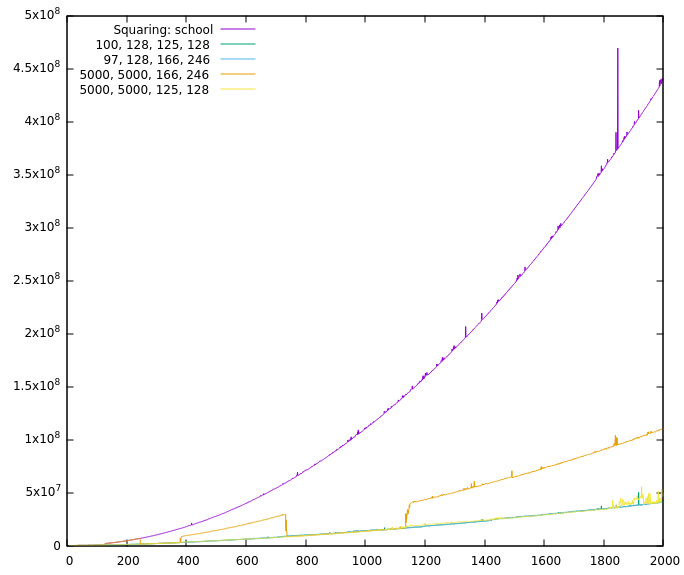
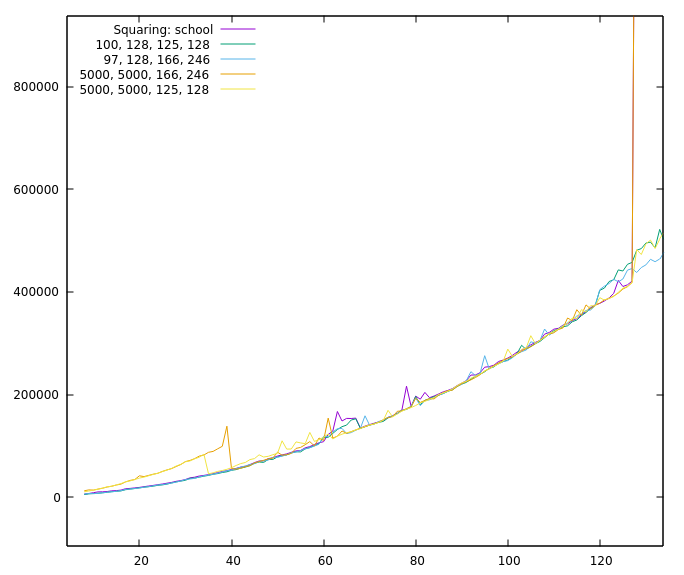
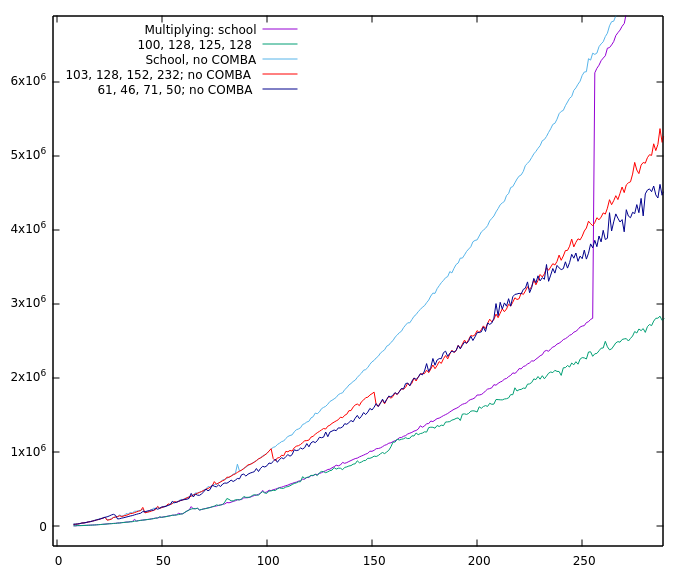
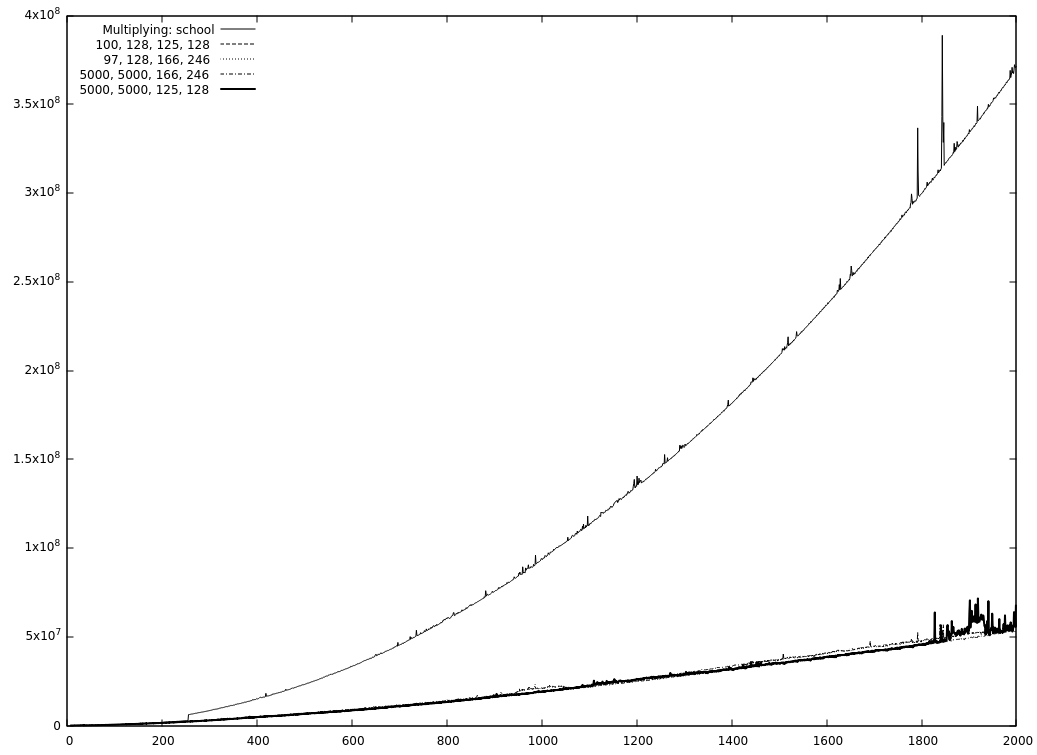

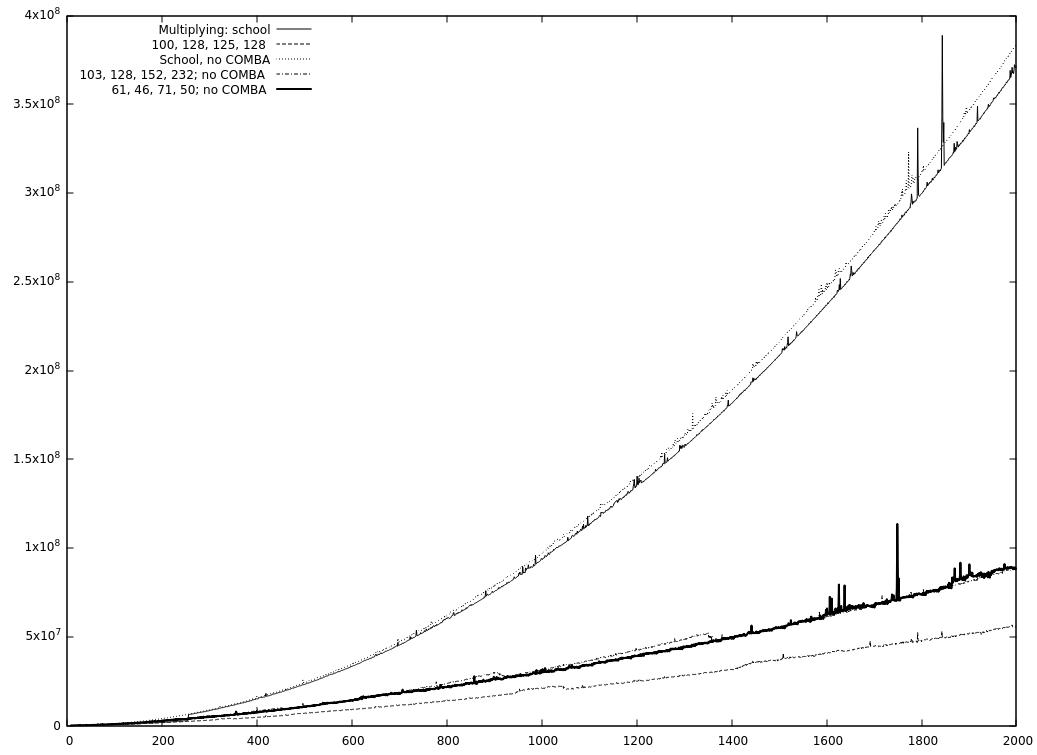
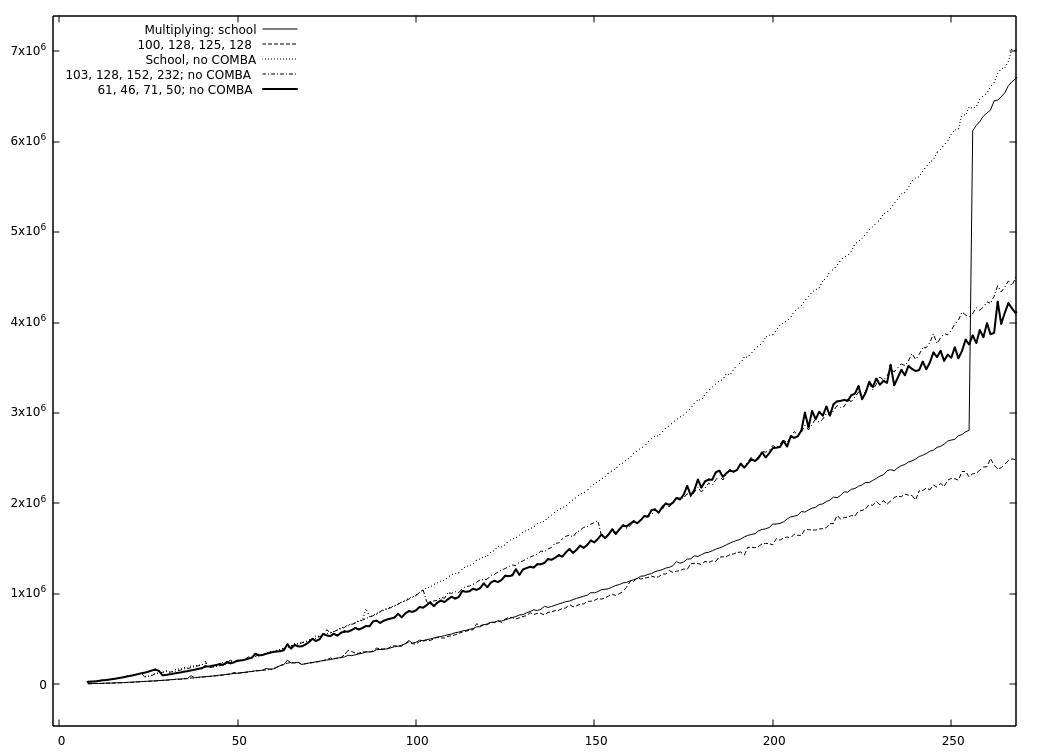
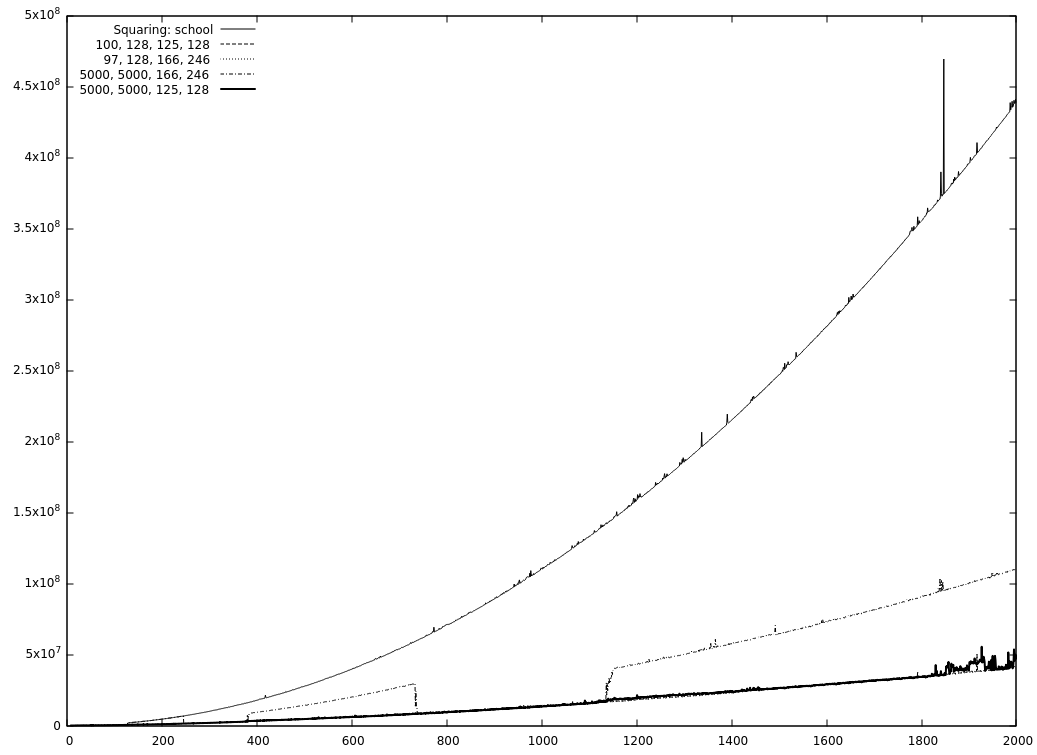
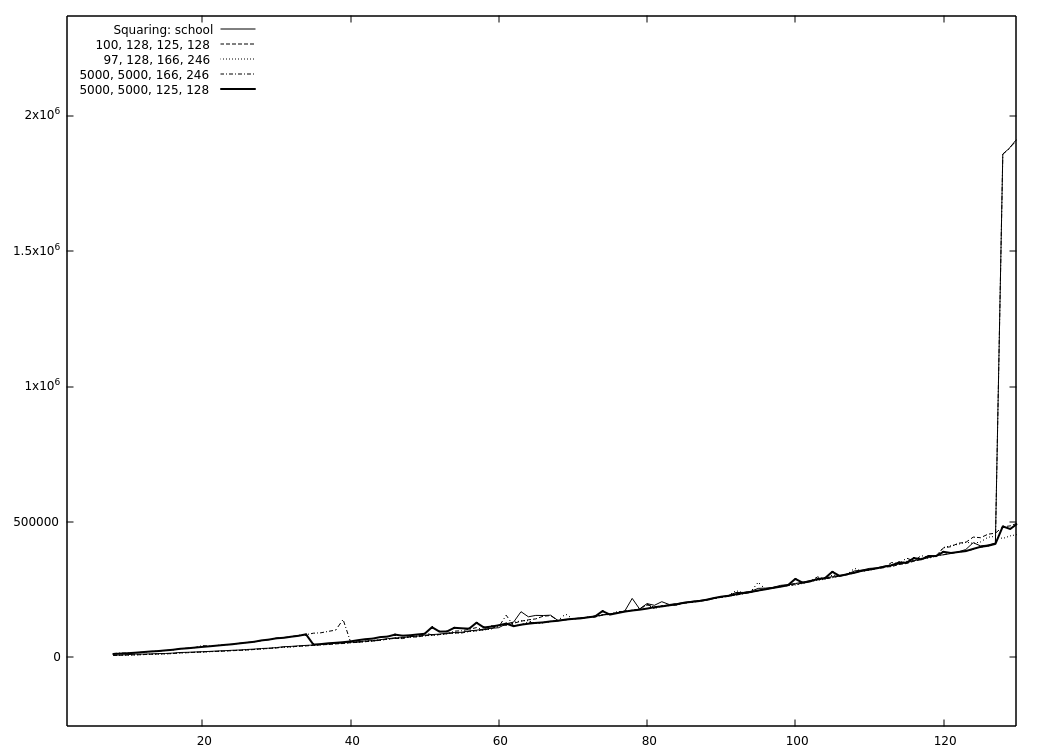
Restarted the work on Toom-Cook 4,5-way and got an irritating first result from
tune.c:Switching off COMBA gave a more reasonable result:
(Yes, it is reasonable that T-C 3-way can be faster than Karatsuba, at least according to Paul Zimmerman and Marco Bodrato)
These values are all below
MP_MAX_COMBA/2for squaring andMP_MAX_COMBAfor multiplication, COMBA is faster than Karatsuba up to theWARRAYlimit, hence the curious results in the very first listing here.The original used the slower algorithms at their benchmarked cut-off points, too, that is without the resetting (as in this PR). With that method and comba switched back on:
These are just the cut-offs and are relative values, COMBA is still faster in its limits! But I haven't measured the actual timings yet to get a better picture, the new functions might have some potential for optimizations (they are not usable otherwise) and there is #447 , too.
This PR gives more realistic results for Toom-Cook 3-way (ignoring the new ones) but doesn't fully solve the underlying problem.
Your opinion?